Authors: Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark
Paper: https://arxiv.org/abs/2404.19756
Repo: https://github.com/KindXiaoming/pykan
Docs: https://kindxiaoming.github.io/pykan/
Twitter: https://x.com/zimingliu11/status/1785483967719981538
Only the lazy have not shared the recent article about KAN these last few days (I am the lazy one). However, there are still not many substantive reviews. Here’s my one.
The authors propose alternatives to the classical multilayer perceptrons (MLPs) named Kolmogorov-Arnold Networks (KANs). The idea is that the fixed activation function for a neuron in MLP is moved to a changeable part and becomes a trainable function (parameterized by a spline) instead of a weight. This seemingly small change leads to a big difference.
Welcome KAN!
If we step back, traditional MLPs rely on the Universal Approximation Theorem (UAT), also known as the Cybenko Theorem, which states that a single-layer feed-forward network with sigmoidal activation functions can approximate any continuous function of several variables to any desired degree of accuracy, provided enough neurons and correct weight selection. There have been many variations of this theorem since. By the way, George Cybenko, the theorem's author, is a living American mathematician and engineer in Dartmouth, where artificial intelligence was born. Well, this theorem is generally useful, giving us a reliable basis for using neural networks.
There is another interesting theorem, the Kolmogorov-Arnold Representation Theorem (KART) or the Superposition Theorem, which states that a continuous function of several variables can be represented as a superposition of continuous functions of one variable. That is, all functions of several variables can be expressed using functions of one variable and addition. Interestingly, in UAT the approximation is close, while in KART it is exact.
Looking at activation flowing through the network, in the case of MLP, they flow through trainable weights (located on the edges of the graph) and reach fixed activation functions (located at the nodes). In the case of KAN, they flow through trainable activation functions on the edges (there are no linear weights as such anymore), and simply sum up at the nodes.
The trainable one-dimensional activation functions on the graph edges are parameterized by B-splines. For a simple two-layer KAN for n inputs, there are 2n+1 hidden nodes where the summation of two functions on the edges occurs, which then sum into one number through other trainable edges. This is simpler in pictures than in text:
This KAN architecture is generalized by the authors to arbitrary network depth and width. The original version of the Kolmogorov-Arnold theorem corresponds to a two-level KAN (can be described by a list of layer dimensions [d, 2d+1, 1]), a more general version of the theorem for deeper networks is unknown, so it is not entirely clear how exactly to deepen and expand. But by analogy with MLP, they suggest a recipe—simply stack more KAN layers! For those who want more technical notation, the work describes the function matrices that describe the KAN layers, as well as the composition of several layers. All operations within KAN are differentiable, so it can be trained with backpropagation.
The activation function is a sum of a base function (playing a role similar to a residual connection) and a spline: ϕ(x) = w (b(x) + spline(x)).
The base function used is silu(x), and the spline is a linear combination of B-splines with trainable coefficients. The trainable coefficient w on top is somewhat redundant, but they kept it for convenience. w is initialized through Xavier initialization, and the spline coefficients—such that the entire spline function is close to zero at the start. The spline is defined over a limited area, but activations can potentially exceed it. Therefore, the spline grid is updated on the fly according to the input activations.
For a KAN of depth L (layers) and with layers of equal width N, and a spline of degree k (usually 3) defined over G intervals (G+1 points), the total number of parameters is O(N2L(G + k)) ∼ O(N2LG). For an MLP of the same width and depth, only O(N2*L) parameters are needed, which turns out to be more efficient. But the good news is that KAN usually requires smaller N, which not only saves parameters but also improves generalization and interpretability.
For increased accuracy, you can perform grid extension—fit a finer spline into a previously coarser one, making the spline node grid more detailed.
KANs have internal and external degrees of freedom. The external ones are the structure of the computational graph, the internal ones are the spline node grid within the activation function. The external ones are responsible for learning the compositional structure of several variables, and the internal ones for learning functions of one variable.
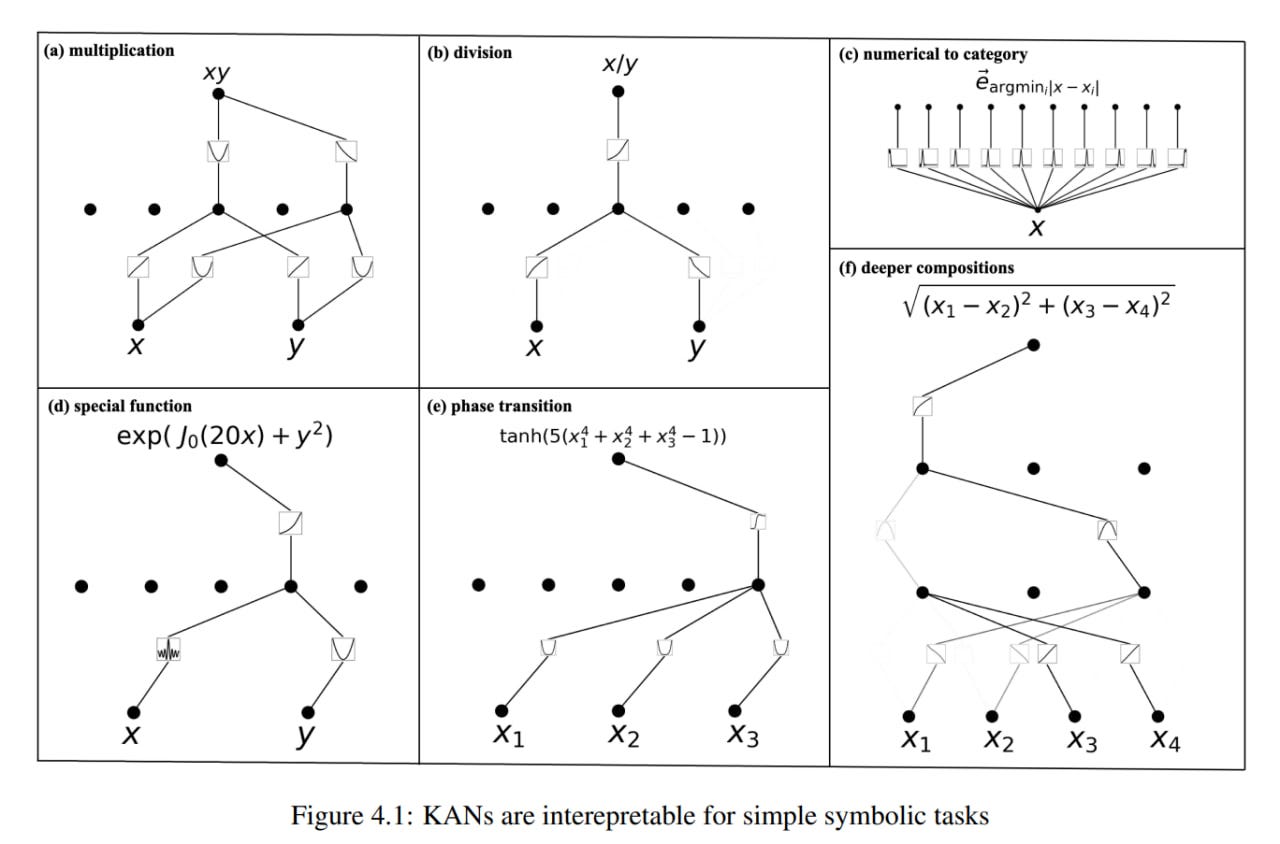
KANs may be useful for interpretability. If we do not know the internal structure of the dataset (what the nature of the data is), we can start with a large KAN, then train it with regularization for sparsity, and then perform pruning. The resulting KAN is better for interpretation. The combination of sparsification, visualization, pruning, and symbolification can help in this matter. In a sense, this replaces symbolic regression, which can help find a symbolic formula describing the data. Here, KAN has an advantage; users can interactively debug and steer it in the right direction.
Experiments
The experimental part is interesting. For regression and PDE solving tasks, the authors showed that KAN is more efficient than MLP. Considering the accuracy of the task solution and the number of model parameters, KAN has a better Pareto front.
First, they tested on five functions known to have a smooth KA representation:
Theoretically, the loss for KAN scales by a power law to the -4th power. In reality, on graphs, it approaches this for simple functions, a bit far for more involved, but is still significantly ahead of MLP, especially with a huge difference in the multidimensional case with a hundred-variable function.
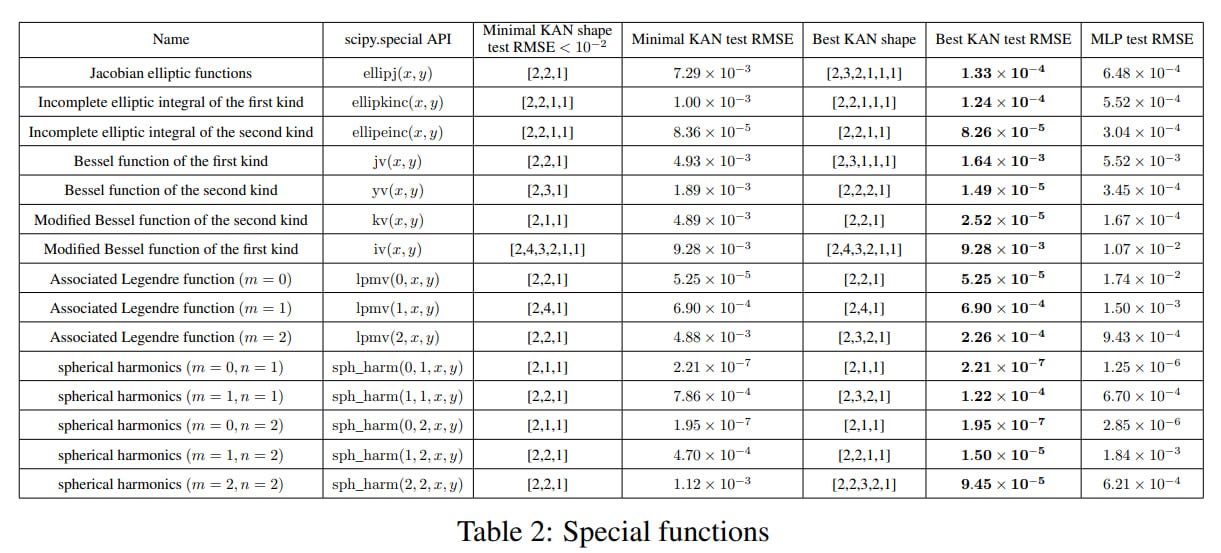
Then, they tested on special functions for which a KA representation is not previously known.
Again, KAN is much more accurate and efficient. Some compact KAN representations are found, which in itself is interesting and could somewhere replace multidimensional look-up tables with a set of one-dimensional ones.
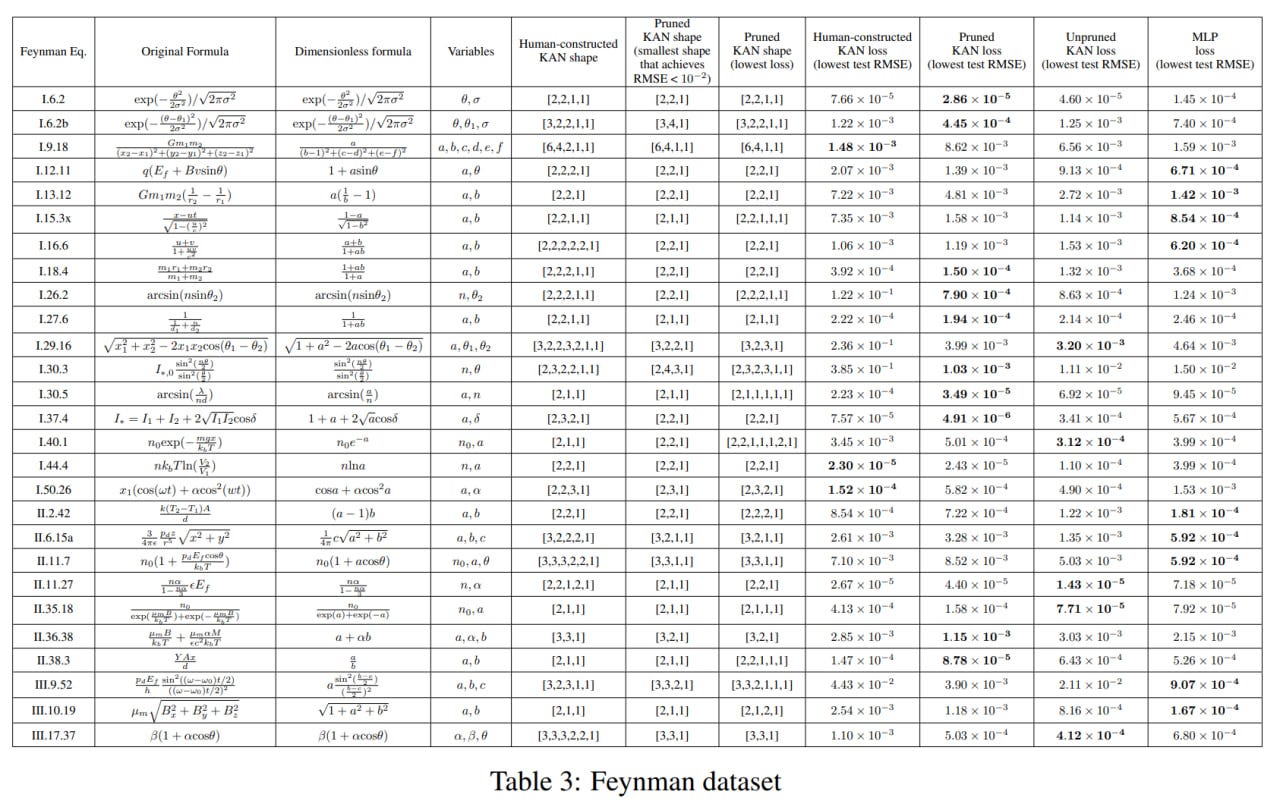
After that, they checked the middle ground, when the exact KA representation is unknown, but we can sketch something by hand based on the nature of the dataset, albeit suboptimally.
Here, you can compare human-constructed KANs and automatically discovered through pruning KANs. For this, functions from the Feynman dataset, collected from equations in his books, were used. Automatically discovered KANs are generally better (smaller) than manual ones. But there is no clear leader overall; somewhere MLP rules, somewhere KAN. The authors believe that the dataset is too simple for this.
In all three tasks, by the way, both KAN and MLP were trained through LBFGS, that is, a second-order method, which is usually not very applicable for training large networks.
In solving PDEs, KAN also shows better scaling curves compared to MLP. Smaller error with a smaller network and fewer parameters.
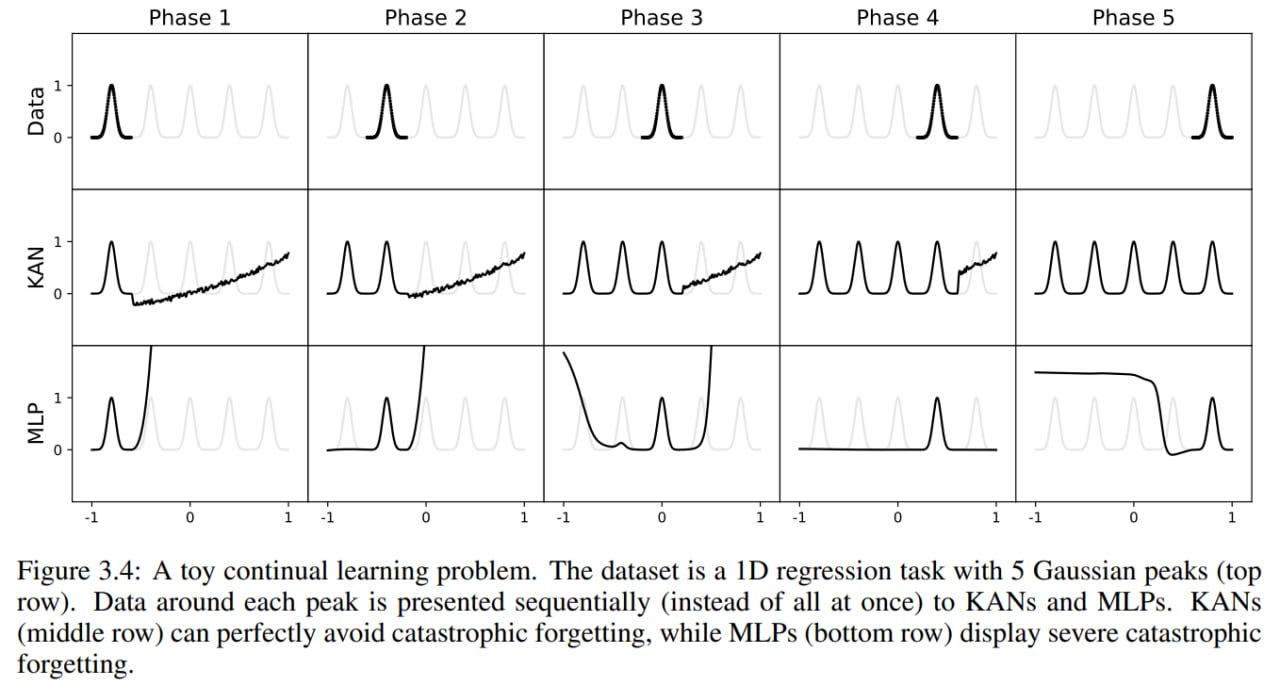
An interesting experiment with continual learning and catastrophic forgetting. On a toy dataset with five consecutive Gaussian pulses presented one after another, KAN does not forget the past, remodeling only the new data region, while MLP fails in an attempt to remodel everything.
A separate chapter is dedicated to the interpretability of KAN.
On simple supervised toy functions such as f(x, y) = xy and slightly more complex ones, KAN after pruning finds an appropriate structure.
On unsupervised toy tasks, KAN can also find groups of dependent variables, which is useful for research.
This approach was applied to the same knot theory problem approached by DeepMind (https://www.nature.com/articles/s41586-021-04086-x). KAN rediscovered the same results with a smaller network and in a more automated mode. Good news for automated science.
The authors go beyond the original DeepMind article, proposing the concept of "AI for Math", where they aim for a broader application of KAN in unsupervised mode to discover more mathematical relations. I'm not an expert in knot theory (not even a beginner), so I can't properly comment on that. Apparently, KAN rediscovered some known things, but didn't discover anything new. The authors hope for deeper KANs in the future.
Another practical scientific task from physics to which KAN was applied is Anderson localization. I'm not well-versed in this yet, but apparently, KAN does quite well.
Besides KAN, the authors also proposed LANs, Learnable Activation Networks. Overall, learnable activations is already quite an old topic, with many works done here. LAN is a simplified version of KAN, or rather a complicated version of MLP with learnable activation functions defined by splines. The activation functions sit at the nodes of the computational graph as in MLP, not on the edges as in KAN. LAN is less interpretable than KAN due to the presence of weight matrices.
Overall, I like the work; it looks like an interesting and useful development of architectures and really something new compared to 100500 perhaps important, but still minor modifications of transformers. Another new thing that is also already happening is the development of SSM and the revival of RNN.
KAN is still only at the beginning of its journey, and the mathematical understanding of them is still very limited. The Kolmogorov-Arnold theorem corresponds to KAN with structure [n, 2n+1, 1], which is a very limited subclass of all KANs (some of which showed interesting results in this work). I expect a flood of work on deepening understanding and applications. At the same time, I expect works in the style of "MLPs strike back", where further changes in MLP improve their results on the listed tasks.
The authors have compiled the code into the pykan library. There is a set of tutorials and a notebook to get started. Docs are here.
The main practical problem with KAN is slow training, usually ten times slower than MLP with the same number of parameters. However, for a quality solution to many of the tasks in the work, fewer parameters for KAN are needed compared to MLPs. And engineering developments will also soon catch up. There are already efficient-kan and FourierKAN libraries. This is just the beginning!