xLSTM: Extended Long Short-Term Memory
A new, improved LSTM by the creator of the original LSTM!
Authors: Maximilian Beck, Korbinian Pöppel, Markus Spanring, Andreas Auer, Oleksandra Prudnikova, Michael Kopp, Günter Klambauer, Johannes Brandstetter, Sepp Hochreiter
Paper: https://arxiv.org/abs/2405.04517
Code: https://github.com/NX-AI/xlstm
Only a few days since we published a review of KAN, mentioning there is also resurrection of RNNs. And voilà! Welcome the extended LSTM, xLSTM!
The authors aim to explore how far language modeling can be advanced using LSTMs by scaling them up to billions of parameters, incorporating all the latest advancements from large language models (LLMs), and eliminating known bottlenecks.
The History
LSTMs have been incredibly successful and stood the test of time. They are the "most cited NN of the 20th century".
Originally created in 1997, LSTMs were designed to address the issue of vanishing (or exploding) gradients. Unlike conventional RNNs, which only had a hidden state (h), LSTMs added a scalar memory cell (now having both c and h) and what was called a constant error carousel (CEC) to update its state, initially featuring a recurrent connection with a weight of 1.0 to its own past state. The original model also had two gates controlling the process: the input gate and the output gate. The input gate protected the memory from irrelevant data, while the output gate shielded other cells from the irrelevant state of the current one. A forget gate was added three years later to allow dropping the memory cell's state when necessary.
However, LSTMs have three main limitations:
The inability to revise the decision to retain data within the memory cell. This is demonstrated with a simple Nearest Neighbor Search task, where a reference vector is provided first, followed by a sequence of other vectors, and the model needs to identify the most similar vector and return the associated value once the sequence ends. The model struggles when an even more suitable vector appears later in the sequence.
Limited memory—everything must fit within a scalar that resides in the LSTM's memory cell. This is highlighted by the task of predicting rare tokens, where perplexity on tokens from the rare bucket in Wikitext-103 is particularly poor.
Poor parallelization due to the sequential processing of hidden states between adjacent time steps. The state depends on the previous one through hidden-hidden connections, referred to as memory mixing.
Enter xLSTM
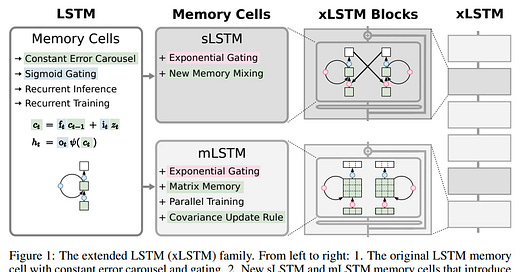
The authors propose Extended Long Short-Term Memory (xLSTM) with two main modifications to the basic equation describing the operation of the standard LSTM. One change involves exponential gates, and the other introduces new memory structures.
From this, two new members of the LSTM family emerge: sLSTM, with scalar memory, scalar updating, and memory mixing, and mLSTM, with matrix memory, covariance update rule through outer product, and no memory mixing. Both versions feature exponential gating.
In sLSTM, exponential activation functions are added to the input and forget gates. Additionally, there's a separate normalizer state, and to prevent things from blowing up, a stabilizer state as well. The memory remains scalar.
Like LSTMs, sLSTM can have multiple memory cells (then memory state is a vector), where memory mixing is possible through recurrent connections of the hidden state (h) and gates with inputs from the memory cell.
sLSTM can also have multiple heads with memory mixing within each head but not between heads. Heads are defined by the structure of a block-diagonal matrix, through which all inputs are processed, with diagonal blocks defining separate heads.
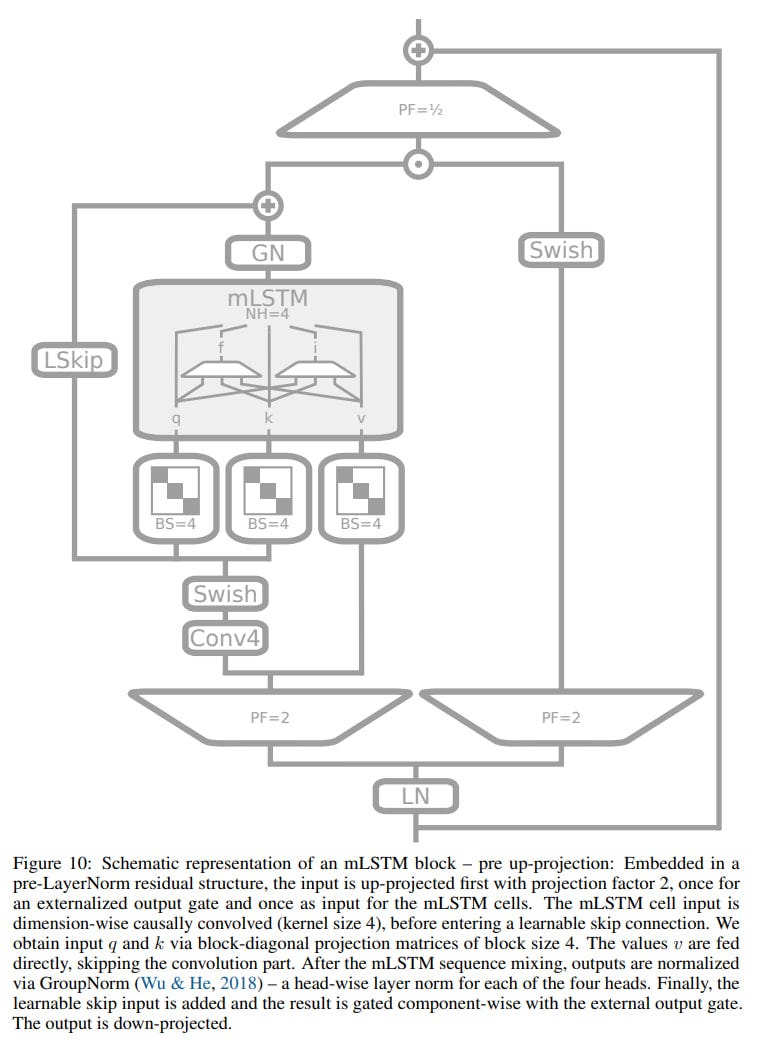
mLSTM (not to be confused with multiplicative LSTM from https://arxiv.org/abs/1609.07959) is more complex. Here, memory is not a scalar but a matrix C of dimension d×d. The authors describe working with memory in transformer terms with query, key, value. Retrieval from memory is implemented by matrix multiplication of C and q. To store k,v (each a vector of dimension d), a covariance update rule is used: C_t = C_{t−1} + v_t * k^⊤_t. LayerNorm is used for k and v to ensure the mean is zero. Like in sLSTM, there are exponential gates, a separate normalizer state, and similar stabilization.
mLSTM can also have multiple memory cells. There is no memory mixing here, and multiple heads are equivalent to multiple cells. Since there are no recurrent hidden-hidden connections, computations can be formulated in a parallel form.
If these new variants are incorporated into residual blocks (with pre-LayerNorm), they become xLSTM blocks, which can be linked together. There are two types of xLSTM block: with post up-projection and pre up-projection. For the first, sLSTM is usually used, for the second, mLSTM (matrix memory works better in high-dimensional space).
The former (post, like in transformers) performs a nonlinear summarization of the past in its original space, then linearly transforms it into a higher-dimensional space, applies a nonlinear activation function there, and translates it back to a smaller space.
The latter (pre, like in SSM) first translates into a higher-dimensional space, performs the summarization there, and then translates it back.
Unlike standard transformers, relative to sequence length xLSTM's computational complexity is linear, and memory complexity is constant. Authors recommend them for edge computing because the memory is compressive. mLSTM parallelizes well, sLSTM does not.
Experiments
The main question is what all this achieves. In the experimental part, the focus is on language modeling.
In the experiments, the notation xLSTM[a:b] is used, where the ratio a/b indicates the number of mLSTM/sLSTM blocks. Thus, if there are a total of 48 blocks in xLSTM, for xLSTM[7:1], it means there are 42 mLSTM and 6 sLSTM blocks.
They first tested on formal language tasks, where the ability to solve state tracking problems should be evident. Baselines are respectable: Llama, Mamba, Retention, Hyena, RWKV-4/5/6. Results confirm that transformers and SSMs are fundamentally less powerful than RNNs (useful video and article for those interested; also see the paper on Chomsky hierarchies). Also, sLSTM outperforms mLSTM.
They then tested on the Multi-Query Associative Recall task, where up to 256 key,value pairs are demonstrated in a sequence and must be remembered for subsequent retrieval. Transformers are the gold standard here, and among all non-transformer models (Mamba, RWKV-5, RWKV-6, xLSTM[1:1], xLSTM[1:0]), xLSTM[1:1] performed best.
In tasks from the Long Range Arena (Retrieval, ListOps, Image, Pathfinder), performance was slightly better than Mamba's and even better than RWKV's.
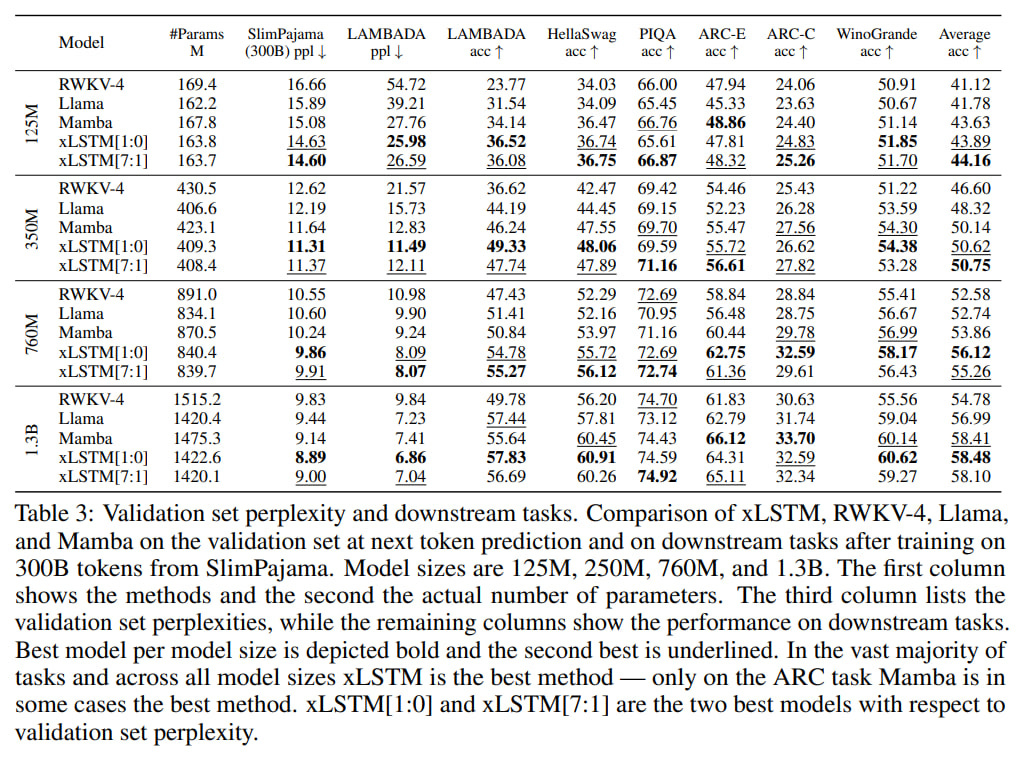
Finally, language modeling. Trained on 15B tokens from SlimPajama, they compared with many fresh models (GPT-3, Llama, H3, Mamba, Hyena, RWKV, RetNet, HGRN, HGRN2, GLA). Unfortunately there is not Griffin, but it’s understandable as its official open implementation does not exist. Models are comparable to GPT-3 with 350M parameters. In terms of final perplexity, xLSTM[1:0] and xLSTM[7:1] are at the top.
The scaling curve (up to 2.7B) looks good, better than Llama, Mamba, RWKV-4.
They made ablations gradually transforming vanilla LSTM into xLSTM. Exponential gates and matrix memory significantly enhance quality.
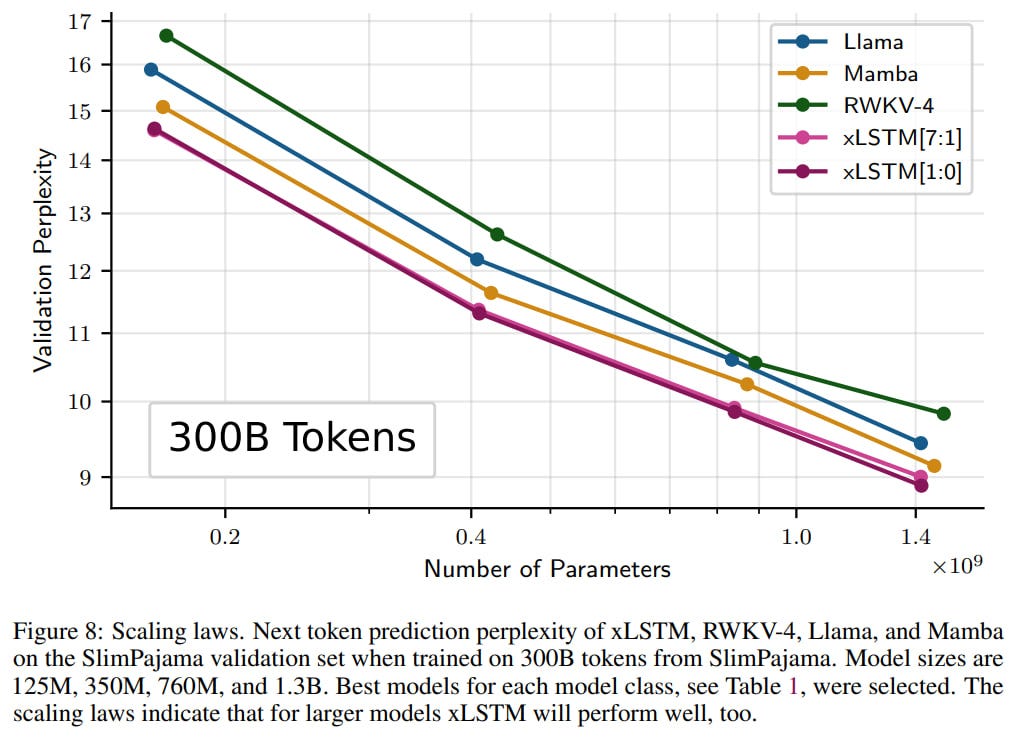
They then increased the volume of training data to 300B tokens (the same numbers used in Mamba and Griffin). In the comparison participated xLSTM, RWKV-4, Llama, Mamba as the best representatives in their classes. Models of sizes 125M, 350M, 760M, 1.3B were trained.
On the trained context of 2048, they checked extrapolation to a greater length, up to size 16384; with xLSTM, all is well.
They then checked perplexity and quality on various downstream tasks. xLSTM leads almost everywhere.
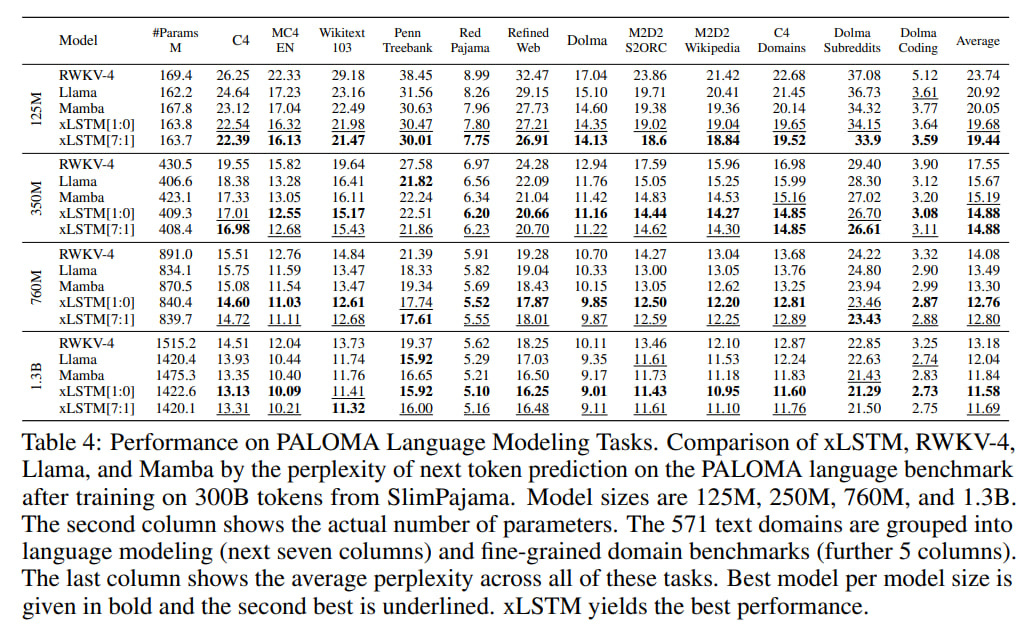
On language tasks from PALOMA, it also performs better than Mamba, Llama, and RWKV-4.
Scales well on 300B tokens too. Of course, it would be interesting to train something gigantic, say 175B. But I understand that not everyone has budgets like OpenAI or Google.
From the main limitations so far, speed (there are also some other nuances listed in section 5 of the paper). sLSTM does not parallelize, but a fast implementation is only 1.5 times slower than parallel mLSTM. The latter is not optimized and about 4 times slower than FlashAttention or implementations through scan in Mamba. But surely everything can be accelerated. On optimization and finding good hyperparameters, there's clearly still a field untapped.
No official code yet, but here are people's attempts to reproduce it, for example, mLSTM (https://github.com/andrewgcodes/xlstm).
So, we have an RNN that looks no worse than transformers and SSM. Eager to see further developments of the idea! And the code.