Authors: Qi Sun, Edoardo Cetin, Yujin Tang
Paper: https://arxiv.org/abs/2501.06252
Blog: https://sakana.ai/transformer-squared/
Code: https://github.com/SakanaAI/self-adaptive-llms
"Transformer-squared" (or Transformer^2, or Transformer2 if you system supports superscript) is a new work from Sakana.ai, a company I deeply respect, especially their founder David Ha. In particular, he co-authored with Schmidhuber the “World Models” paper that kickstarted a new wave of work on World Models (more on this topic here). David consistently participates in various non-mainstream interesting works, like Hypernetworks or Weight Agnostic Neural Networks. I highly recommend keep an eye on his work. They also recently released the widely discussed AI Scientist. They're also working on nature-inspired algorithms and artificial life. If you're in Japan or planning to move there, consider this lab-company in Tokyo — they've raised a Series A round and are actively hiring.
TL;DR
Transformer2 is an interesting approach to LLM adaptation, an alternative to fine-tuning and LoRA in particular.
In brief, the idea is that we decompose all weight matrices of trained LLM weights through SVD, and then fine-tuning/adaptation involves scaling the singular values of this decomposition — amplifying some singular components while dampening others. This creates different "experts" with varying mixes of singular components present in the model. Learning coefficients for singular values requires significantly fewer parameters than full fine-tuning or even LoRA. Moreover, these coefficients can be found at test-time, where in the first forward pass we analyze the task and determine the topic (how to adapt these coefficients = which experts are needed to solve this task), and in the second forward pass we simply apply the necessary coefficients (activate the required experts) and solve the task.
Transformer2
Now for the details.
The traditional approach to adapting a pre-trained model is fine-tuning, also known as post-training. Conceptually it's simple — collect data and retrain — but in practice it's resource-intensive, requiring significant time and compute. Self-adaptive models are more flexible. Instead of training an LLM for all tasks in one step, you can independently develop expert modules and add them to the model as needed. The MoE (Mixture-of-Experts) direction is currently very popular, with one of the recent solutions being Self-MoE (https://arxiv.org/abs/2406.12034), but current MoE approaches are still mainly predetermined before training and trained classically.
Transformer-squared approaches this from a slightly different angle. Regular fine-tuning deals with modifying weight matrices obtained during training that contain sufficiently rich information to solve various tasks. Instead of trying to add new features, fine-tuning should focus on revealing these latent capabilities and making them more pronounced. In other words, we need to find what experts already exist in the model (even without MoE) and learn to apply them to relevant tasks by modifying weights right at test-time.
Singular Value Fine-tuning (SVF)
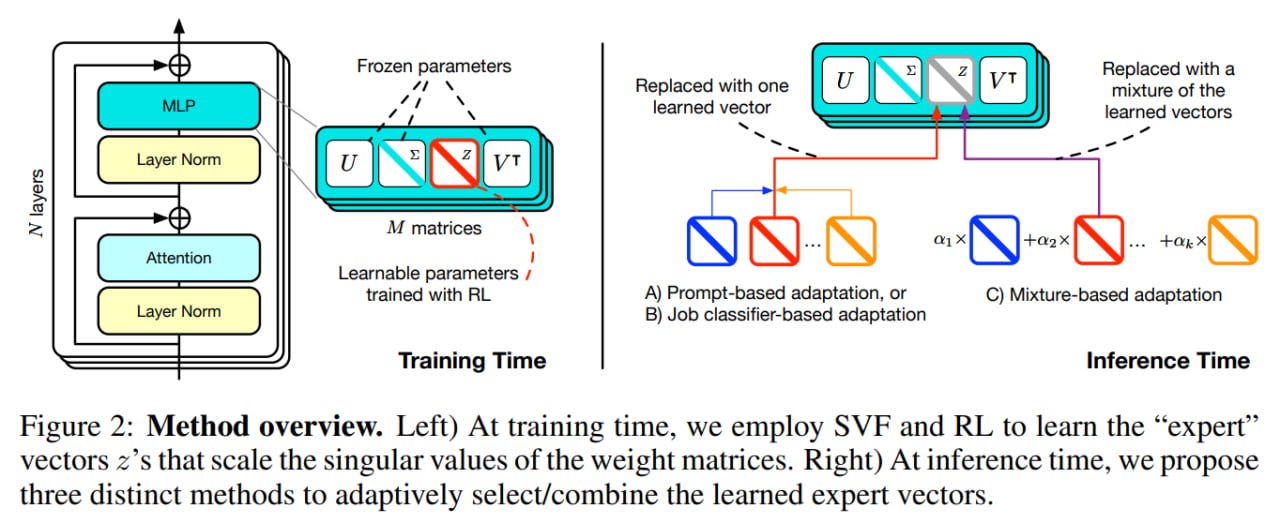
Transformer^2 is built on Singular Value Fine-tuning (SVF), which provides efficient parameterization for fine-tuning and enables compositionality for adaptation. During training, SVF is performed, followed by self-adaptation during inference.
SVF does this as follows.
First, as I understood from the code, each weight matrix W of the pre-trained model is decomposed via SVD into:
W = UΣV'.
There's nothing exotic here, just pure U, S, V = torch.svd(v).
For those not familiar with SVD (Singular Value Decomposition), it's an extremely useful linear algebra algorithm. Some good resources are here (text) and here (video).
Second, to implement SVF, a small modification is made to the obtained matrices in the form of a vector z of dimension r (number of singular values), which purposefully modifies individual singular values by multiplying them by corresponding components of vector z. So finally, SVF looks like:
W* = UΣ*V', where Σ* = Σ ⊗ diag(z).
The training objective here is to find a set of these z-vectors, one for each downstream task. Each z-vector can be thought of as an expert specializing in specific task. It determines the strength of each specific singular component obtained after SVD. Some components are weakened, others are strengthened.
The set of SVF vectors z is found through RL using the good old REINFORCE algorithm with KL-regularization on deviation from the model's original behavior. Apparently, SVF's regularization capabilities help RL avoid typical failure modes, prevent it from defaulting to next-token prediction training, and enable learning from a small number of examples.
This approach has several advantages:
Fine-tuning is simplified because for each task, you only need to find the values of vector z (r numbers) without touching all other weights. LoRA requires (m+n)×r', where m and n are the dimensions of the original weight matrix, and r' is a hyperparameter (LoRA rank) which must be large enough for expressiveness (can go up to 256, see https://huggingface.co/blog/mlabonne/sft-llama3). SVF requires r = min(m, n). This might seem to lead to less expressiveness, but the ability to influence a full-rank weight matrix provides more information than low-rank methods.
Compositionality improves. The weights of the original matrix are broken down into independent singular components, resulting in the learned vector z also becoming more composable and interpretable. LoRA doesn't have such properties (although, perhaps, there is some composability of LoRA adapters).
The ability to change the magnitude of existing singular components provides an effective form of regularization with the possibility of fine-tuning on tasks with hundreds of points without risk of serious collapse or overfitting. I'm not entirely sure how this directly follows, as with large coefficients in polynomials, for example, you can definitely overfit.
Test-time adaptation
After training on a set of predefined tasks, we can perform adaptation on a specific example and its related task at test-time. Adaptation consists of the following. This is a two-pass algorithm that combines K experts — z vectors trained through SVF. In the first pass on a given task or prompt, Transformer^2 looks at its inference behavior and determines a z' vector optimized for current conditions (selects the best expert). This z' is used in the second inference pass to obtain the final answer using the new adapted weights.
The paper proposes three different approaches to determining z'.
Prompt engineering. A special adaptation prompt is created, which the LLM uses to categorize the input prompt. Depending on the response, one of the categories used for pre-training experts in SVF and its corresponding z' is extracted. If none fits, there's a generic "others" category, in which case the base weights are used without modifications.
Classification expert. A special classification system is used. Following the best traditions of language compiler development, where at some point the language compiler is written in the language itself, the base LLM is fine-tuned through SVF to solve this task. A special classification expert zc is trained on a dataset with K tasks. Then zc is loaded in the first inference pass and thus makes a better determination of who should be used in the second pass.
Few-shot adaptation. A new z′ is computed as a weighted combination of existing learned SVF vectors. The coefficients α_k for these vectors are found through the Cross-entropy method (CEM) on a set of few-shot prompts. This only needs to be done once for each target task, and unlike classical few-shot prompting, there's no need to increase the size of the working prompt by adding examples.
Results
What are the results of the squared transformer?
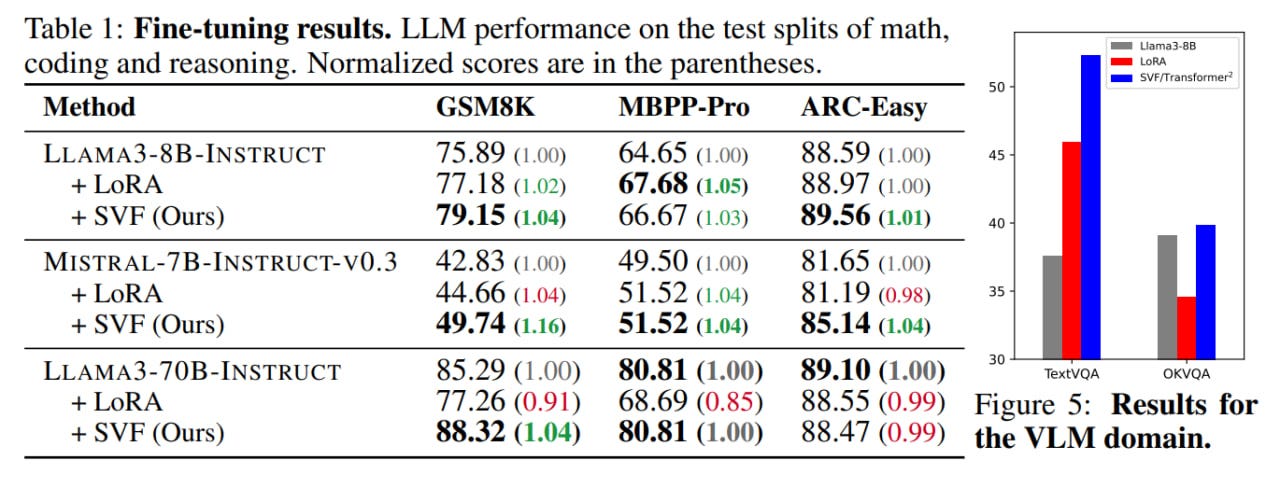
They took three LLMs from a couple of different families: Llama3 8B Instruct, Mistral 7B Instruct v0.3, and Llama3 70B Instruct.
For each model, they find three sets of z-vectors for GSM8K, MBPP-pro, and ARC-Easy tasks respectively. That is, mathematics, program synthesis, and reasoning. For Llama3 8B, they also trained a vector for TextVQA.
On corresponding test sets, SVF shows stable improvement, often surpassing LoRA with rank 16 (these were trained on next token prediction; they tried with RL too, but RL LoRA performed worse than SVF). The authors believe this is due to RL — its training objective doesn't require perfect solutions for each example, unlike in LoRA's case. SVF is also more parameter-efficient, with the number of trainable parameters being less than 10% of LoRA.
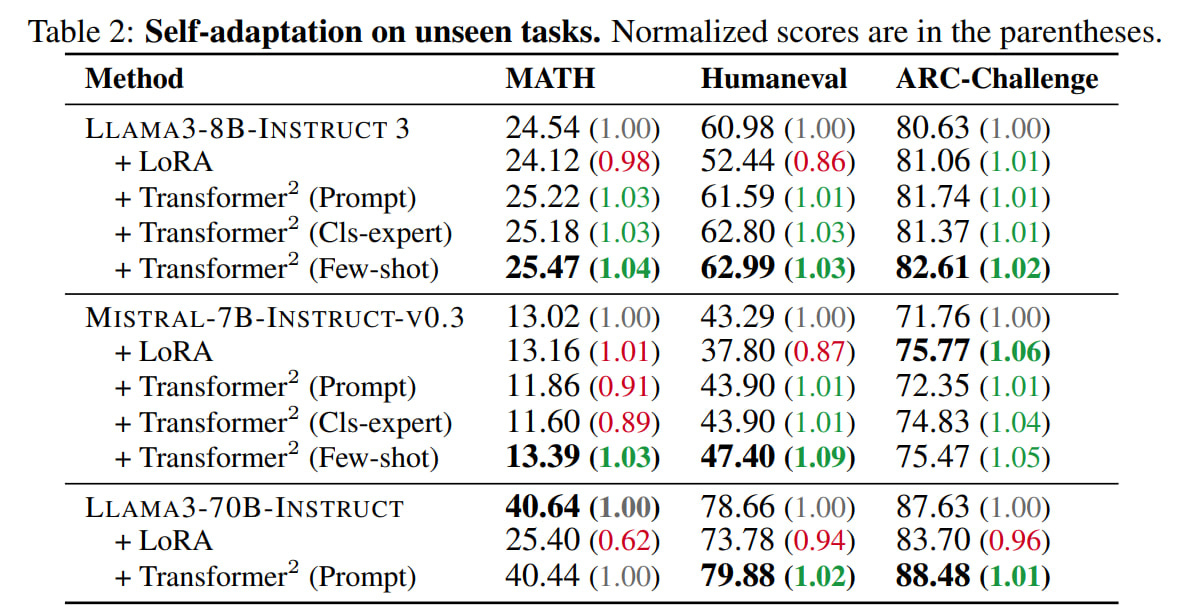
After training SVF and obtaining z-vectors, they evaluated adaptation quality on new tasks. They evaluated on MATH, Humaneval, ARC-Challenge, and OKVQA tasks. LoRA results here are practically negligible (all worse), while Transformer2 shows improvement almost everywhere. The Few-shot adaptation method performs best. Interestingly, even on the VLM task with vectors trained on completely different text tasks, Transformer2 shows notable improvement. Apparently, it's really useful parameterization.
The visualization of individual α_k vector weights for the third adaptation variant is interesting. For example, when solving MATH problems, there's no dominance of weights from GSM8K; for Llama3 8B, almost half of the contribution comes from ARC weights. Other tasks and models also show non-trivial mixes.
For the first and second adaptation variants based on classification, confusion matrices show that examples match well with experts trained on corresponding domains.
The second pass typically takes significantly longer than the first in terms of inference time, and the first pass's contribution relative to the second, depending on the task (in reality, on the number of generated tokens), ranges from 13% to 47%.
Ablations showed that applying SVF to both attention and MLP provides a boost — more to MLP, but it has more weights, and it's better to apply to both simultaneously. The RL objective gives much better results than next token prediction. And LoRA with RL performs worse than SVF with next token prediction.
An interesting experiment involves transferring expert vectors between different LLMs. Transferring vectors from Llama to Mistral improves results on two out of three tasks. On ARC-Challenge, it even outperforms Mistral's own results. This is potentially an interesting result that needs further investigation.
Overall, it's an interesting work. I like the parameterization itself; it's elegant and understandable. It might even add something to interpretability. And the fact that it works better than LoRA is, of course, excellent. Although LoRA still maintains an advantage in terms of speed, as it doesn't require two passes. But perhaps in the era of test-time scaling, this isn't so important anymore.