Transformer Layers as Painters
Authors: Qi Sun, Marc Pickett, Aakash Kumar Nain, Llion Jones
Paper: https://arxiv.org/abs/2407.09298
Twitter: https://x.com/A_K_Nain/status/1812684597248831912
Code: https://github.com/floatingbigcat/transformer-as-painter (not yet)
The second paper on creative approaches to transformer layer computation follows LayerShuffle. In this more radical approach from my GDE fellows, layers aren't just shuffled.
The authors propose an intriguing metaphor for the network's intermediate layers—an assembly line of painters. The input canvas passes through a chain of painters, some specializing in birds, others in wheels. Each painter decides whether to add something or pass it along unchanged. They share a common dictionary for understanding drawings, so it's not disastrous if a painter receives a canvas from an earlier stage. They can also be swapped with little catastrophe (even if background parts are drawn over existing objects). Painters can even draw simultaneously in parallel.
This analogy isn't scientifically precise but raises many questions: Do layers use a common representation space? Are all layers necessary? Do all intermediate layers perform the same function? Is layer order important? Can layers be computed in parallel? Is order more critical for some tasks than others? Does looping help parallelized layers? Which variations harm performance the least?
Good questions. Previous works like LayerDrop and LayerShuffle cover only a small part of this.
LayerDrop was tested on ViT, and this work on pre-trained LLMs (decoder-based Llama2 7B with 32 layers and encoder-based BERT-Large 340M with 24 layers) with no fine-tuning (except for GLUE evaluation, implying fine-tuning for BERT). Llama was tested on ARC (AI2's ARC, not François Chollet's ARC-AGI), HellaSwag, GSM8K, WinoGrande, and LAMBADA. BERT was tested on GLUE.
Results show that the initial and final layers are crucial, while the middle layers are more resilient to such manipulations. It seems the middle layers use a shared representation space.
Examining the cosine similarity of layer activations within the model suggests there might be more layer groups: input layer 0, layers 1-3, middle layers, and the last or last few layers. The model might have three different representation spaces for the initial, middle, and final layers.
Skipping M layers (dropping layers from N+1 to T-N, where T is the total number of model layers) gradually degrades quality as M increases, indicating that not all intermediate layers are necessary—at least a few middle layers can be dropped without catastrophic degradation.
Replacing the middle layers with a copy of the central layer results in much worse performance than simply dropping them, the most significant degradation in the study. This suggests that middle layers perform different functions. The appendix further examines cosine similarities and activation statistics, concluding that repeating a middle layer pushes the input out of the shared representation space. If a painter specializes in wheels, drawing more wheels on the canvas forces subsequent painters to work with elements they haven't been trained on.
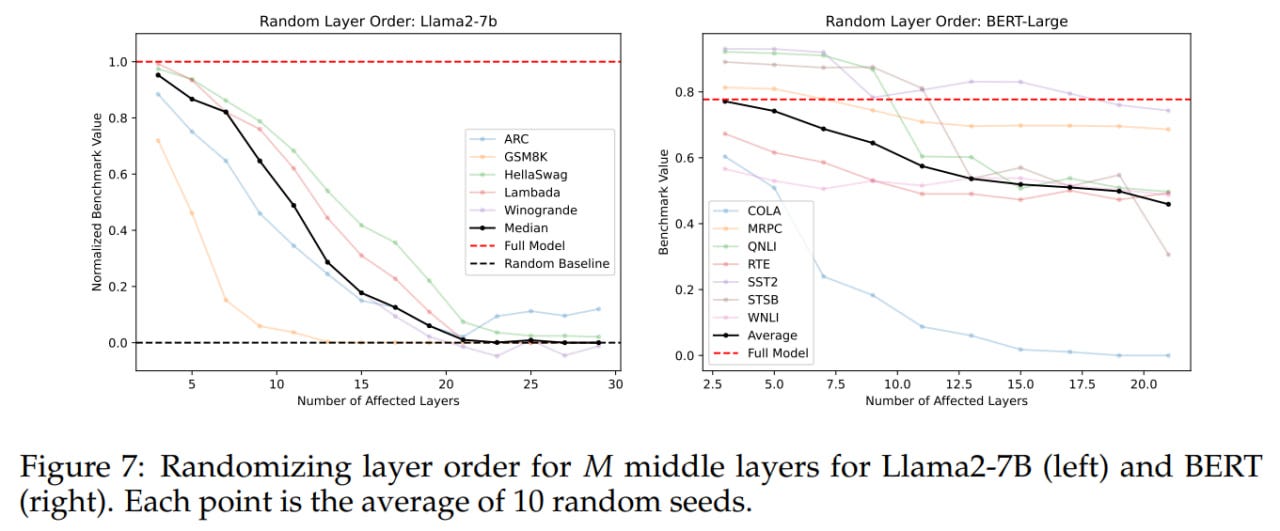
Thus, while middle layers share a representation space, they perform different operations within it. So, does layer order matter? To test, the middle layers were executed in 1) reverse or 2) random order (averaged over 10 seeds). Both cases show gradual degradation, with random order faring better than reverse. This indicates that the sequence does matter to some extent. Both randomizing and reversing the middle layer order has graceful degradation.
An interesting question arises: can layers be computed in parallel and then merged (via averaging)? Again, we see gradual degradation except for GSM8K, where performance drops sharply. This approach is better than skipping layers but worse than reverse order. Parallel execution is viable except for math-heavy benchmarks.
Some benchmarks show worse drops than others, primarily with abstract (ARC) and mathematical (GSM8K) tasks. Step-by-step reasoning tasks seem more sensitive to layer order than semantic tasks because reasoning involves both structure and semantics. An arithmetic example shows the parallel version maintains the overall thought structure, but calculation errors arise. In the painter metaphor, semantic tasks are like drawing a collage where order matters less, while sequential tasks are more like a precise architectural scene. Regardless of analogy, math and reasoning tasks depend more on layer order than semantic tasks.
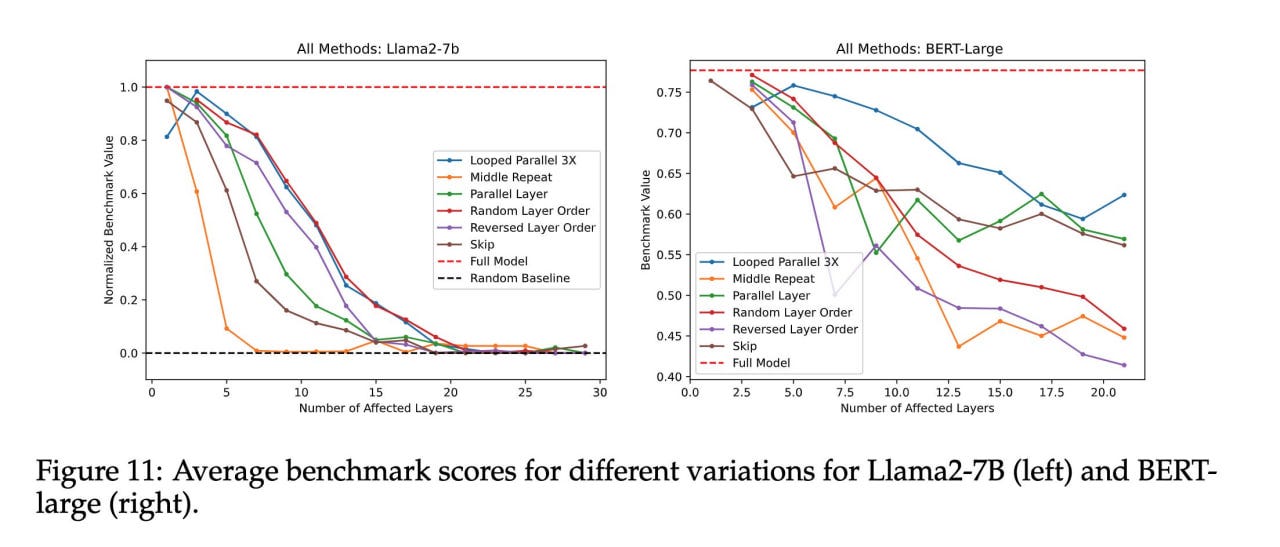
Extending the painter metaphor, some painters might only be ready to draw when there's an appropriate input. So, a wheel-specializing painter may not draw without seeing a car body first. The previous parallel layer computation experiment can be improved by looping these layers. Feeding the aggregated output back as input to the parallel layers for a number of iterations shows three iterations are much better than one. A broader analysis indicates the optimal iteration number is roughly linearly proportional to the number of parallel layers.
Across all analyzed variations, repeating a single layer causes the most degradation. Random order and parallelization with loops are the least harmful.
Overall, this is a well-written, easily readable paper that could be replicated by anyone in their garage, not requiring Google-level resources. It's exciting to see room for independent researchers. In the future, the authors aim to look deeper into why transformers are resilient to such variations. One hypothesis is that residual connections in training are necessary for layers to share representations. It will be interesting to test models without such connections. They also plan to unfreeze models and observe how quickly they recover during fine-tuning. Parallel computation and layer skipping are advantageous latency-wise, offering practical benefits. Another potentially interesting topic is routing for layer selection, similar to Switch Transformers (https://arxiv.org/abs/2101.03961).