Thermodynamic AI is getting hotter
Title: Thermodynamic Computing System for AI Applications,
Authors: Denis Melanson, Mohammad Abu Khater, Maxwell Aifer, Kaelan Donatella, Max Hunter Gordon, Thomas Ahle, Gavin Crooks, Antonio J. Martinez, Faris Sbahi, Patrick J. Coles
Paper: https://arxiv.org/abs/2312.04836
Blog: https://blog.normalcomputing.ai/posts/2023-11-09-thermodynamic-inversion/thermo-inversion.html
The work from Normal Computing introduces a new class of hardware: the thermodynamic computer and stochastic processing unit (SPU). The paper describes the first such device that successfully implements one of the fundamental operations in linear algebra widely used in ML, matrix inversion.
There are earlier works on Thermodynamic AI by the same team, such as “Thermodynamic AI and the fluctuation frontier” (https://arxiv.org/abs/2302.06584) with a blog post about it, and “Thermodynamic Linear Algebra” (https://arxiv.org/abs/2308.05660).
An even earlier work, “Thermodynamic Computing” (https://arxiv.org/abs/1911.01968) from a broader author collective, reflects the outcomes of a workshop on the topic.
Thermodynamic AI in a nutshell
The idea is that the building blocks of such hardware are stochastic and ultimately make software inseparable from the hardware (similar to Hinton's concept of Mortal Computers).
Unlike quantum and analog computers, noise here is a necessary resource for computations.
A significant number of ML algorithms are based on various physics principles, like energy-based models or diffusion models. Stochasticity is universally used, from weight initialization, through neural network building blocks (like dropout), to generation procedures (such as diffusion models, VAE and GANs). For such algorithms, natural stochastic fluctuations can become a crucial resource.
The new building blocks include stochastic bits (s-bits), whose state randomly evolves over time as a continuous time Markov chain (CTMC). Since not everywhere bits are needed (neural network weights or feature values are more like real numbers), the building block can correspondingly represent a continuous variable. Hence, the fundamental building block of Thermodynamic AI hardware is the stochastic unit (s-unit) - a continuous variable undergoing Brownian motion. This can be implemented on an analog electrical circuit with a noisy resistor and capacitor.
The authors aim to unify modern AI algorithms, many of which share two commonalities: 1) they use stochasticity, 2) they are inspired by physics. Hence, the proposal is to unify such algorithms based on thermodynamics. Examples of thermodynamic algorithms include generative diffusion models, Hamiltonian Monte Carlo, and simulated annealing. A mathematical framework (described in the aforementioned work “Thermodynamic AI and the fluctuation frontier“, and in general, for more details, you should look there) can be formulated where these algorithms are special cases.
Thus, the same thermodynamic hardware could accelerate all these algorithms. Profit!
Enter SPU
Returning to the current work, it presents the first continuous-variable (CV) thermodynamic computer. The authors created a stochastic processing unit (SPU) that fits on a circuit board.
It contains 8 cells, each an LC circuit with a Gaussian noise current source (implemented on FPGA). The cells are all interconnected. For customization, each cell has not one, but a battery of four capacitors to choose from. The noise level and sampling frequency (with a base frequency of 12 MHz) at which cell voltages are read can also be adjusted.
On the resulting SPU, one can sample from an 8-dimensional Gaussian distribution.
Another useful primitive is matrix inversion. The mathematics of the process was described in another aforementioned work (“Thermodynamic Linear Algebra”). For this, matrix elements are converted into connections of a system of oscillators, and after the system reaches thermodynamic equilibrium, voltage values are taken (sampled many times) and a covariance matrix is calculated, which in turn is proportional to the inverse matrix to be found.
Initially, a 4x4 matrix was inverted on the SPU, requiring only a subset of the cells. The more samples taken, the lower the error, but it never reaches zero (imperfection of the experiment).
Then an 8x8 matrix was inverted. This was done on three independent SPUs, showing that they yield similar results, thus the process is reproducible.
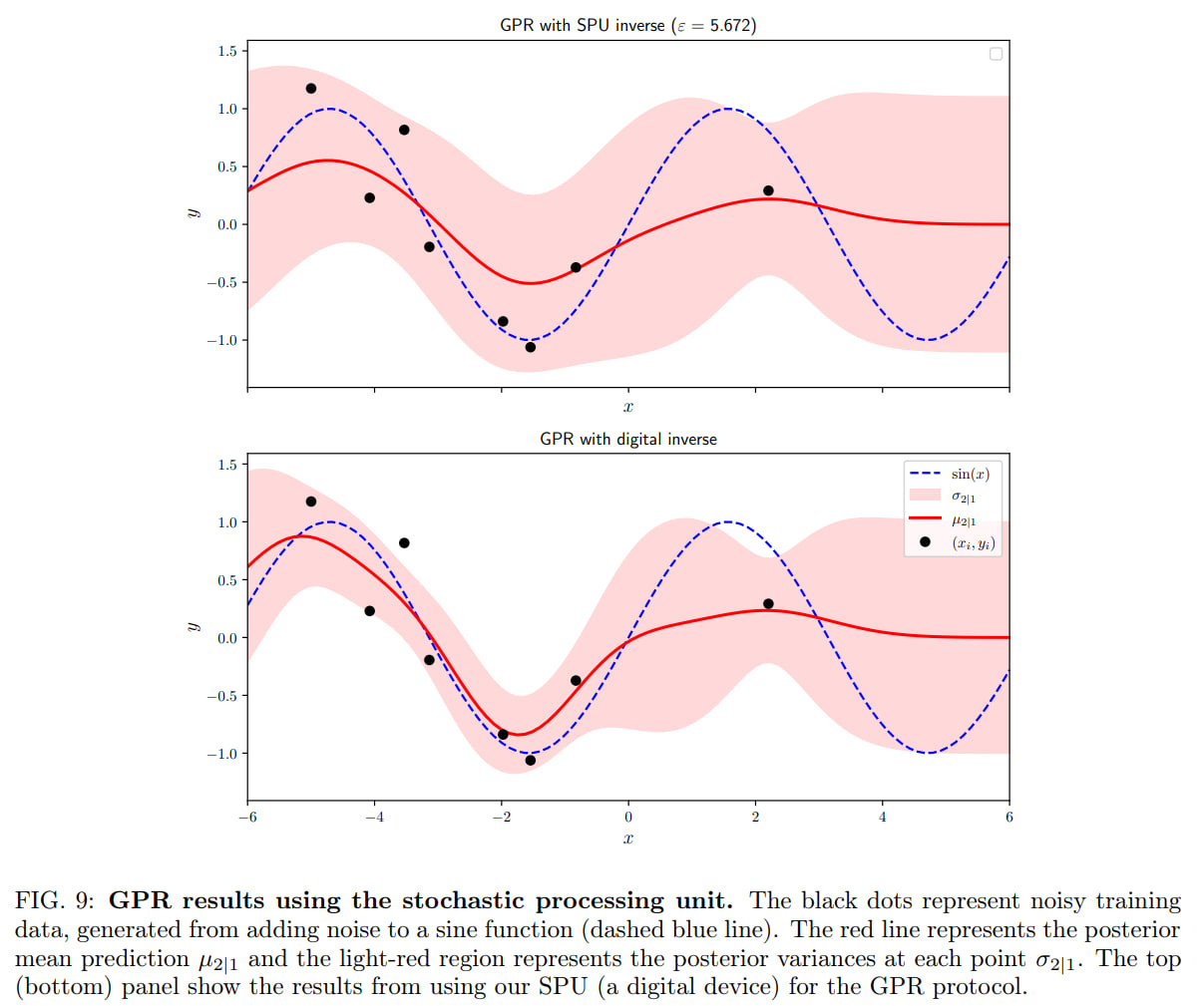
The SPU also implemented Gaussian process regression
and Uncertainty quantification through spectral-normalized neural Gaussian processes for neural network class prediction. The SPU's results are well aligned with those calculated on a digital computer.
The authors expect that on a large scale, the SPU will have advantages over classical hardware. To demonstrate this, they compared the SPU with the RTX A6000 GPU on the task of sampling from a multidimensional Gaussian distribution. At a large number of dimensions, the SPU performs better than classical methods on the GPU. The intersection point of the two curves (the so-called “thermodynamic advantage”) is around 3000 dimensions. Overall, the asymptotics for the SPU is estimated as O(d2), while for Cholesky sampling on the GPU it is O(d3). In terms of energy consumption, the SPU is also better.
In short, it's an exciting direction. The field is in its infancy, and there is potential to contribute to the discovery of new interesting algorithms for this new hardware, just as there was with algorithms for quantum computers. Training neural networks on such new hardware is still a long way off, but who knows how quickly we can get there.

















Love this innovation at compute level and its direct meaningful implementation of core ML algo which is most expensive to compute. My gut feeling, this combined with Stanford living matter lab research by Dr Ellen can help model many aspects of life biology, chemistry and physics in a computationally efficient method and system. Many ADC converters like brain on chip by Cortical labs can be potentially be replaced with these analog circuitry for natural interface like using "touch" .