Stochastic activations
Divine benevolence or fundamental physics? The mysterious world of activation functions
Maria Lomeli, Matthijs Douze, Gergely Szilvasy, Loic Cabannes, Jade Copet, Sainbayar Sukhbaatar, Jason Weston, Gabriel Synnaeve, Pierre-Emmanuel Mazaré, Hervé Jégou
Paper: https://arxiv.org/abs/2509.22358
There are still people in this world who continue digging into low-level details (this time activations)! But they still tie everything to LLMs. It’s so unusual to read in the introduction that an activation function is what sits inside an LLM between two linear layers in an FFN block. We used to explain this more simply, using the example of a single neuron...
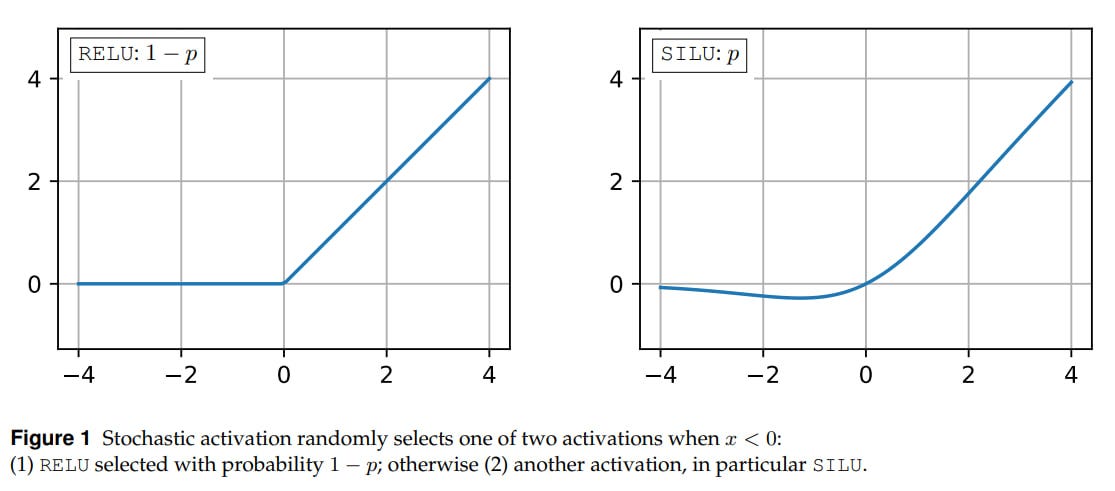
The authors propose stochastic activations. At first, based on the title, I thought it would be about something slightly different, that there would be some clever function with randomness, like RReLU (randomized rectified linear unit, where a random small linear coefficient was chosen for the negative part), but it turned out they’re proposing randomly choosing between SILU and RELU (which of course can also be considered a stochastic function, but here the stochasticity is elevated to a higher level), and this approach has its advantages.
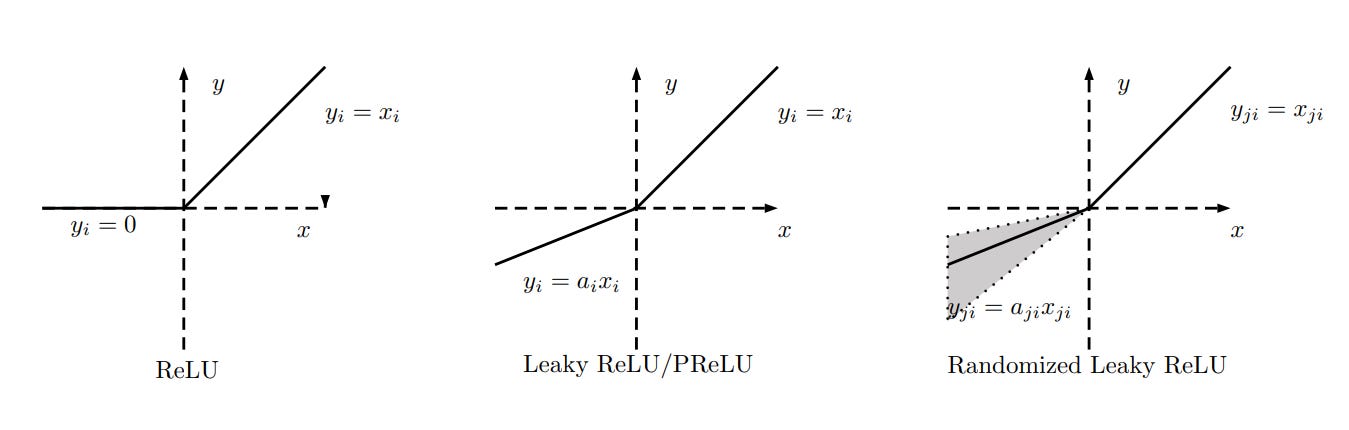
RELU (=max(x, 0)) as we know was good, helped rapidly advance the entire field somewhere around the AlexNet era, when it turned out that networks learned much faster with it than with differentiable classics like sigmoids and hyperbolic tangents. The problem with RELU was that if the activation is in the negative argument zone, the gradient there is zero and it can’t escape from there. This is precisely why networks with RELU also naturally demonstrated a tendency toward sparsity, which in turn is good if the hardware can more efficiently multiply sparse matrices (but this didn’t appear immediately, and it still may be challenging for such a sparsity).
SILU (Sigmoid Linear Unit, also known as swish, =xσ(x)), especially in combination with gates (SwiGLU), consistently beat RELU in quality, but didn’t provide sparsity. Perhaps it beat it precisely because RELU had zero gradients in a large number of cases, and this prevented the network from learning well.
There were also a million other functions. From relatively recent ones, for example, Adaptive SwisH (ASH), with stochastic sampling inside. Somewhere ideologically near sparsity also lies Dropout, including structured variants like LayerDrop (we mentioned this here).
The question then is classic: how to address RELU’s limitations while preserving all its advantages?
“If the mouth of Nikanor Ivanovitch could be placed under the fine nose of Ivan Kuzmitch, and add to it the grace of Baltazar Baltazarovitch, and perhaps also a little of Ivan Pavlovitch’s good manners, then it would be easy to make my choice. But as it is—how and whom am I to choose?”
— from Gogol’s “Marriage”
Two approaches are proposed:
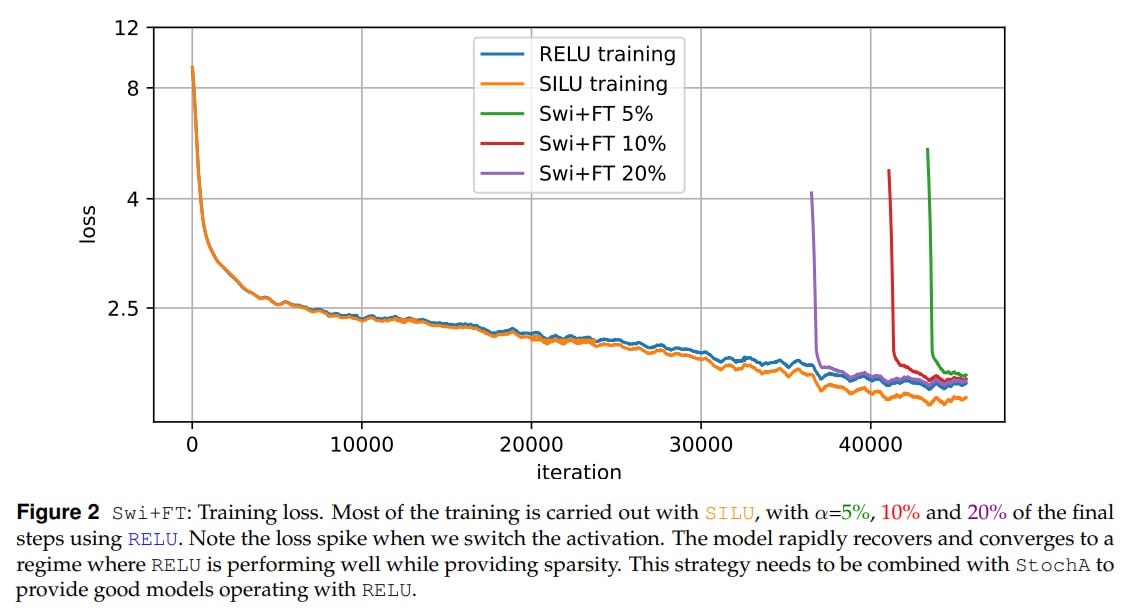
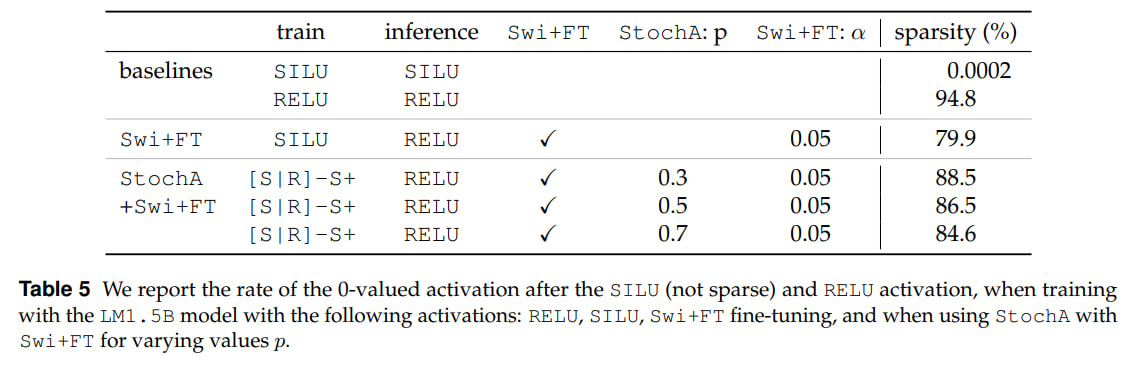
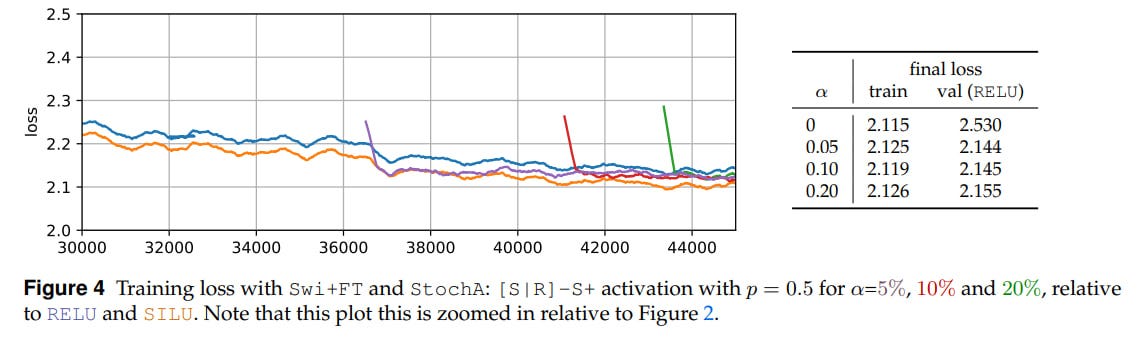
Swi+FT — activation fine-tuning: you train an LLM with one activation (a higher quality one), then replace it with RELU and fine-tune. More precisely, during training for the first
1−αof the total number of steps, a good activation is chosen (SILU for example), and then we switch to the second one (RELU). The value ofαis usually around 5-10%, sometimes they try 20%. At inference, we also keep the second activation. There’s no optimizer warm-up, its parameters are not reinitialized, but a cosine schedule is applied, where the learning rate smoothly decreases to 0.01 of its peak value. Since SILU and RELU are similar (identical asymptotes and value at zero), no problems arise. There’s a spike in the loss at the moment of switching, but it quickly goes away.StochA — proper stochastic activations: activations are randomly chosen from a given set, either in training or in testing. Here a Bernoulli (binary) random variable
ω ∼ Bernoulli(p)is used, so with probabilitypone function is chosen, and1-p— another. This, by the way, also resembles activation dropout (even though dropout is for a different purpose), since it turns out that with a given probability we choose a function that will zero out the negative argument.
An alternative strategy is to randomly choose between identity (y=x) and the zero function (y=0) with probability given by the sigmoid, which in expectation gives SILU. In practice, it doesn’t work very well.
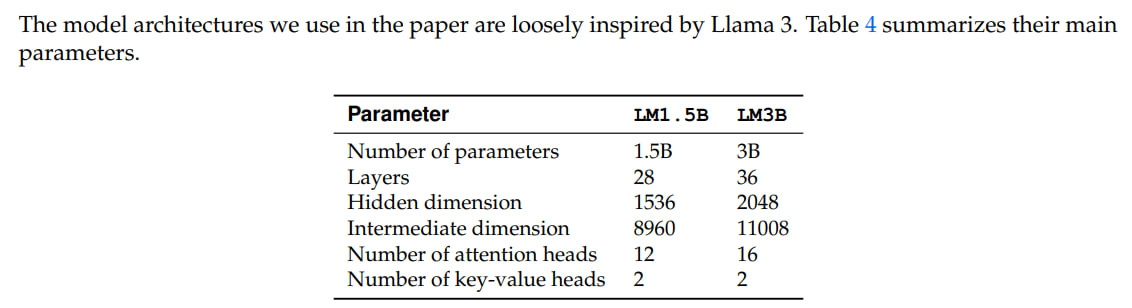
They train dense decoders with GQA, RMSNorm + pre-norm, RoPE. Models are 1.5B and 3B. Optimizer is AdamW. Llama3 tokenizer, vocabulary of 128k + 256 reserved tokens. Pre-training on 47B and 80B tokens, mainly English texts and code. Batch of 1M tokens, context of 8k.
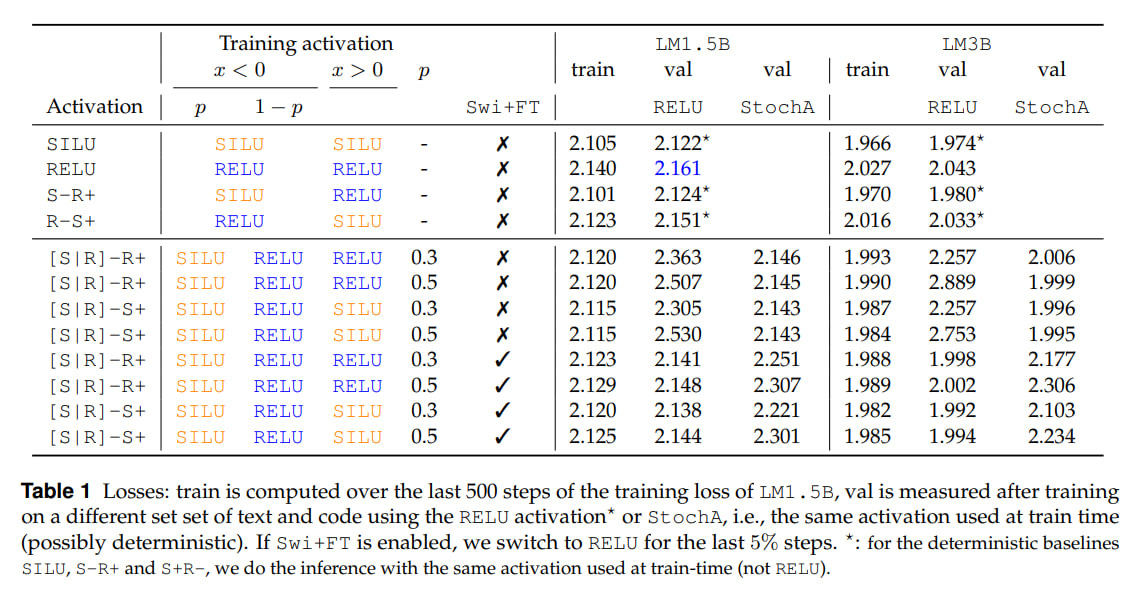
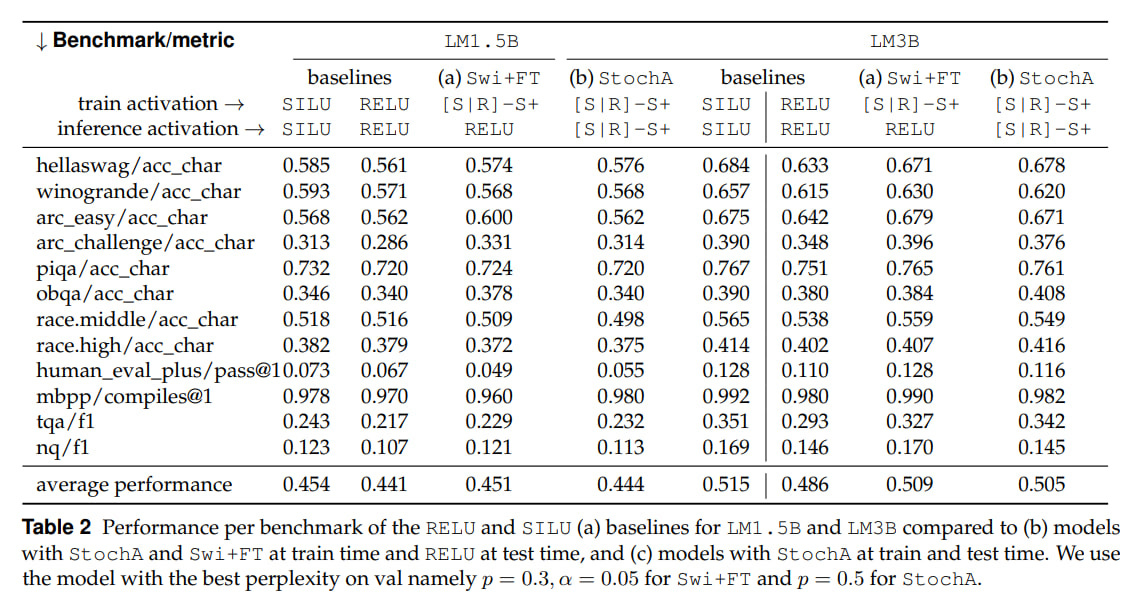
Stochastic activation gives slightly lower loss on training compared to RELU. But SILU gives even lower loss. Without fine-tuning, everything drops on validation, but after it, it’s fine, but again, as far as I can see, not better than deterministic SILU.
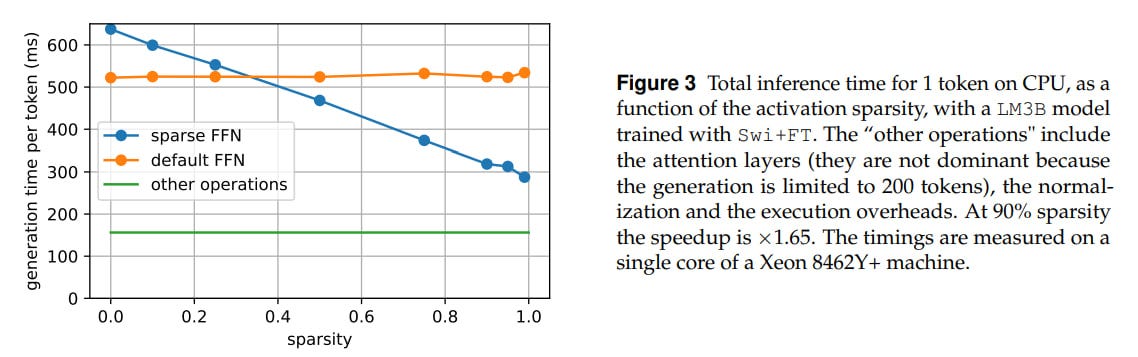
When using RELU at inference, sparsity can exceed 90%, which in theory allows not loading 90% of the weights from memory. Sparsity of 90% gives a 65% speedup of inference on CPU. On GPU, you still need to somehow make the computations predictable enough to balance the load between CUDA threads.
This part is actually one of the most interesting, but there aren’t many details here. How exactly did they implement the computations on CPU? If the bottleneck is memory access, then you still need to read first to understand that there’s a zero there, right? Or immediately do sparse computations and for specific multiplications use some library for sparse linear algebra with the correct storage format. Was there a procedure for converting a dense model to partially sparse for inference? They mention storing different matrices by rows or columns, but I want more meat about sparse FFN.
It’s interesting that with fine-tuning, if you use both Swi+FT and StochA simultaneously, there’s a spike on the loss graph at the moment of switching to RELU, but then it goes away and the final model quality is higher than if it had initially been trained on RELU. At the same time, if you use only Swi+FT, the final result is worse. And they’re still worse than deterministic SILU.
Another curious observation: at test-time you can use StochA instead of RELU and without fine-tuning (!). It works reasonably well, the result is between RELU and SILU (see Table 1 above). You can use this to generate multiple answers for a single prompt.
On downstream tasks, the picture is similar. The new methods are better than RELU, but worse than SILU. So the main selling point is the potential speedup due to sparsity, 1.65x for CPU (and for GPU you still need to work on it, but in theory for Nvidia GPUs of the last several generations with sparsity support in tensor cores it should work somehow). If you need quality, then SILU is better without question. Or the popular SwiGLU, which is SILU with a gate. There’s also the often-used GELU, although it seems to me people have been moving away from it toward SwiGLU (Sebastian confirms).
There are probably some other newer activation functions as well, but I haven’t seen a modern comparison of all of them like the good old one for CNNs or Noam Shazeer’s study on transformers. There was ReLU2 for sparse LLMs, where it beat everyone. There was xIELU, which also seems better than SwiGLU. We’re waiting for someone to do a full-scale comparison again.
Probably, here once again we can end with a quote from Noam Shazeer from that 2020 work:
We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence
In general, it’s unclear, maybe globally this is all unimportant and minor details, but maybe something fundamental is hiding behind this that we haven’t yet understood, basic physical laws.
By the way, Noam had a keynote talk at the recent HotChips:
Everything with his involvement is worth watching and reading! Let me also remind you that he’s a co-author of the paper on transformers, T5, papers on MoE, etc. An example of a very cool person without a PhD.
Let’s end on that note.




"Divine benevolence or fundamental physics?"
--
Grigory, don't tell God what to do