By Amund Tveit, Bjørn Remseth, Arve Skogvold
Paper: https://arxiv.org/abs/2504.16041
Here's an interesting story about grokking, specifically about the impact of optimizers and how switching from AdamW to Muon significantly accelerates the onset of grokking.
To grok or not to grok
As a reminder, grokking is a fascinating generalization phenomenon where a model first appears to overfit (high accuracy on the training set but random-level performance on the validation set), but if training continues, at some point the performance on the validation set quickly rises to high values. The model suddenly "gets it" or “groks it”. In case you didn’t know, Heinlein has invented the term.
The current work defines grokking as follows: it's the first epoch where validation accuracy reaches or exceeds 95% after training accuracy has stabilized around 100%.
If you haven't read the original grokking paper (https://arxiv.org/abs/2201.02177), I highly recommend it. Those were the days when OpenAI published interesting papers like this one, the double descent work (https://arxiv.org/abs/1912.02292), and many others...
Muon
Muon (MomentUm Orthogonalized by Newton-Schulz) is a fresh optimizer (https://github.com/KellerJordan/Muon) designed for training internal layers of models, working with 2D+ parameter matrices. Different vectors and scalars need to be trained with something else, like AdamW. People empirically found that embeddings and classification heads are also better trained without Muon, as they have different optimization dynamics (at least the embeddings do).
The algorithm takes gradients from SGD-Nesterov-momentum (it can work without Nesterov, but performs better with it) and post-processes them through a Newton-Schulz iteration, which approximately orthogonalizes the update matrix. More details about the algorithm can be found here: https://kellerjordan.github.io/posts/muon/.
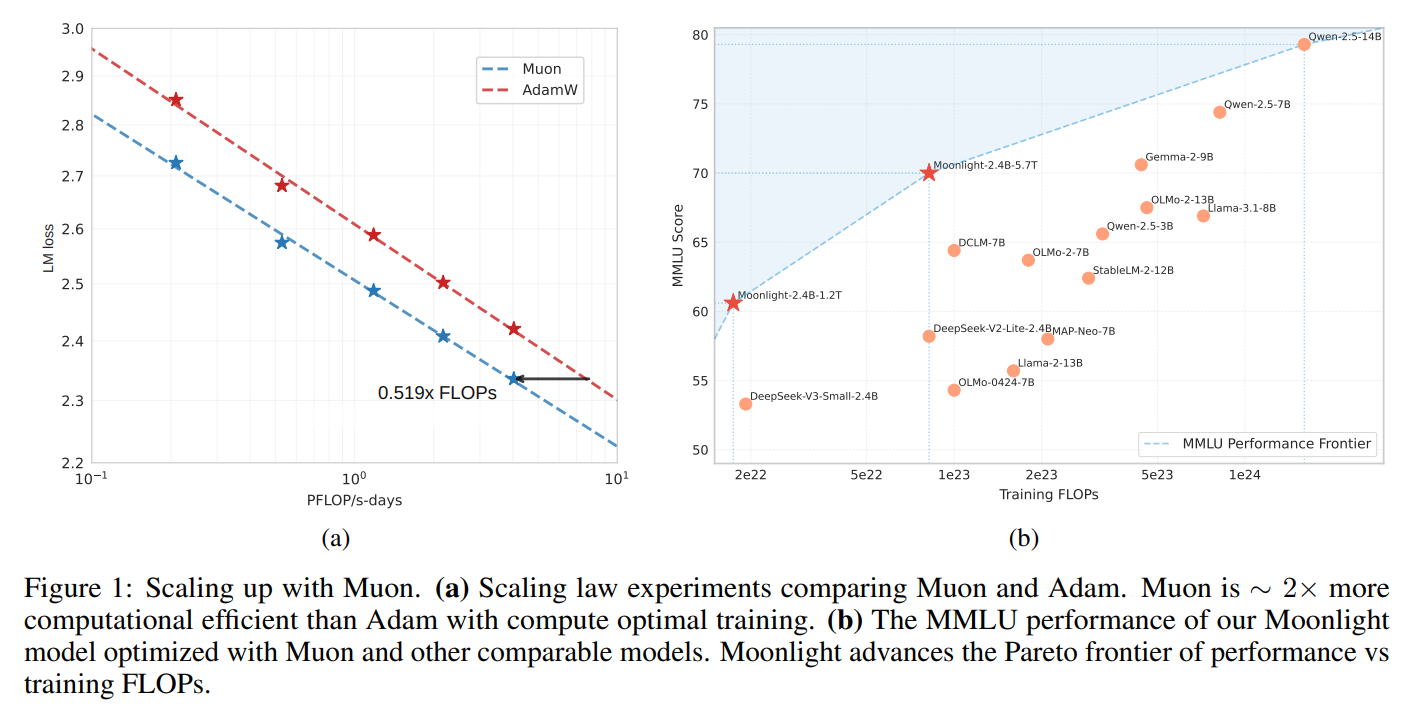
Muon was born in the fall of last year and has already proven effective for scaling MoE LLMs from 3B/16B parameters (a variant of deepseek-v3-small) in training on 5.7T tokens, being approximately twice as efficient as AdamW (https://arxiv.org/abs/2502.16982).
Grokking faster
In the current work, several datasets were tested. The dataset from the original grokking paper with modular arithmetic mod 97, as well as a dataset on parity of 10-bit binary strings. These tasks were chosen because they clearly demonstrate the phenomenon.
Since one of the recent papers on grokking (https://arxiv.org/abs/2501.04697) showed the influence of softmax instability (Softmax Collapse) on the phenomenon, they tried several alternatives: standard Softmax, piecewise linear Stablemax with better stability, and Sparsemax which leads to sparse results.
They tested on a classic transformer, with identity embeddings (token "42" maps to vector 42), RoPE, RMSNorm, SiLU activations, with dropout.
They compared AdamW (β1 = 0.9, β2 = 0.98) and Muon, running multiple experiments with different random seeds.
As a result, Muon has a statistically significant advantage, leading to grokking much earlier, around the 100th epoch instead of the 150th. The distribution of grokking times is also narrower.
So if you want fast grokking, use Muon!
The authors speculate about what exactly in Muon helps grokking. Spectral norm constraints and second-order cues steer the model away from simple memorization and help discover the true pattern.
In general, broader research is needed on larger models and diverse tasks.
New optimizers are an interesting topic in general, with constant innovations and new theories emerging. For example, one recent paper "Old Optimizer, New Norm: An Anthology" (https://arxiv.org/abs/2409.20325) generalizes several methods (Adam, Shampoo, Prodigy) and shows their equivalence to steepest descent with a specific norm, as well as outlining a new space (choice of norm, choice of step) for designing such algorithms. This conceptually resembles the approach that SSM authors continually reproduce, using increasingly general mathematical apparatus to bring different methods (RNN, SSM, transformers) under one umbrella. I haven't studied the paper closely yet, but it looks interesting. And it also discusses Newton-Schulz iteration.
Thanks to the authors of Muon, I found a wonderful quote in Noam Shazeer's 2020 paper (https://arxiv.org/abs/2002.05202):
"We offer no explanation as to why these architectures seem to work; we attribute their success, as all else, to divine benevolence."
On this optimistic note, I'll conclude.