Authors: Shawn Tan, Yikang Shen, Zhenfang Chen, Aaron Courville, Chuang Gan
Paper: https://arxiv.org/abs/2310.07096
Prehistory: UT and MoE
In the realm of neural network architectures, the Universal Transformer (UT) has held a special place in my technical heart. Originally discussed in this article in my other blog on Medium (as a part of a series on Adaptive Computation Time, or ACT, in neural networks), the UT concept was a step beyond the conventional Transformer model, aka Vanilla Transformer (VT).
To recap the UT's concept in brief: unlike the VT, which employs a series of diverse layers each with its unique weights, the UT innovatively utilizes a single layer. This layer is repeatedly applied, feeding its output back into its input, thereby iteratively updating the input embeddings. This process is governed by a unique 'readiness' predictor, controlling the output through the prediction of a 'pondering value.' The process halts when this cumulative value surpasses a certain threshold. Intriguingly, this mechanism operates at the individual token level, allowing more complicated tokens to be processed longer than their simpler counterparts.
Since its introduction in 2018, several studies have illuminated the UT's efficacy. One notable study highlighted the VT's generalization issues, which were not present in some other architectures, particularly when dealing with Chomsky's hierarchies (https://arxiv.org/abs/2207.02098). Further research, such as “The Devil is in the Detail: Simple Tricks Improve Systematic Generalization of Transformers” (https://arxiv.org/abs/2108.12284), demonstrated the UT's superior generalization capabilities. However, the UT encounters certain scaling complexities. Some findings (https://arxiv.org/abs/2104.06022) indicated a higher demand for training and memory in the UT on WMT tasks, with subsequent scaling curves (https://arxiv.org/abs/2207.10551) affirming these challenges.
This is where the Mixture-of-Experts (MoE) architecture comes into play, aiming to mitigate the computational demands of larger models. It functions by activating only certain portions of the network at any given time, for example, a select few 'experts' from a larger pool. When not all experts (E) are chosen from the available pool, but rather a subset (k), this is termed a Sparse Mixture of Experts (SMoE). Notable implementations of SMoE include the Switch Transformer (https://arxiv.org/abs/2101.03961) with k=1 and GShard (https://arxiv.org/abs/2006.16668) with k=2.
The advent of the Sparse Universal Transformer (SUT), which integrates UT with Sparse Mixture of Experts (SMoE), marks a new milestone in this ongoing journey.
Here comes SUT
The current SUT research applies SMoE independently to Multi-Head Self-Attention (MHSA) and Feed-Forward (FF) layers. Within the FF layers, the typical SMoE approach replaces a single layer with a set of FF layers (experts), from which the top-k experts are selected. For MHSA, the study employs Mixture of Multihead Attention (MoMHA) from “Mixture of Attention Heads: Selecting Attention Heads Per Token” (https://arxiv.org/abs/2210.05144), selecting the top-k attention heads from all available. A specialized gating network oversees the selection of experts, issuing a distribution from which the top experts are chosen. Together, these two SMoE components constitute the SUT block, which is then reused across all layers of the new transformer model.
Training this sophisticated architecture necessitates additional loss functions. The approach here involves maximizing a specific unsupervised version of Mutual Information Maximization (MIM) loss for training the gating network. This loss function not only enables a sharp distribution for expert selection but also balances expert workload, ensuring a uniform selection across the batch scope.
In this work, a unique version of Dynamic Halting, distinct from the UT, is employed, based on the stick-breaking process (a concept derived from the Dirichlet process, more details available on Wikipedia). Initially, a specialized MLP (Multi-Layer Perceptron) predicts halting probabilities based on embeddings from the previous layer. Following this, the halting probability for each layer is calculated, considering none of the preceding layers have halted. If the cumulative halting probabilities don't exceed a threshold (0.999), the process continues. The attention mechanism in this context might refer to either a halted layer or one still being calculated, so the embeddings must be taken from either the last computed layer or the current one.
The SUT formulation also introduces a special ACT (Adaptive Computation Time) loss, aimed at minimizing the number of layers being computed.
Experiments
The approach was tested across various tasks, with noteworthy outcomes.
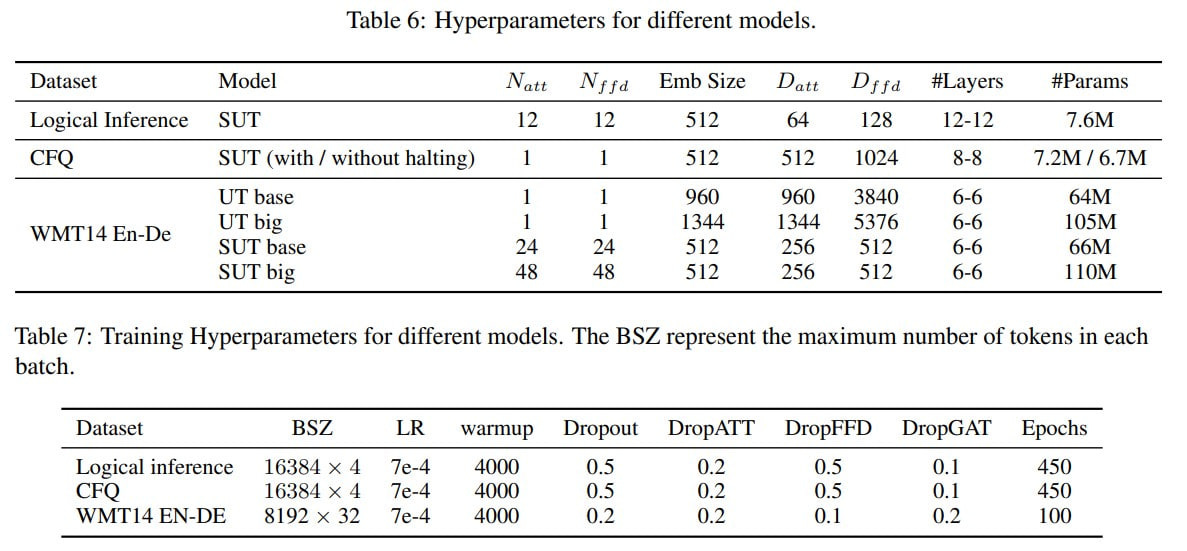
WMT’14 English-German Translation Task: Both UT and SUT, with an unspecified number of experts (E=24/48, k=?), performed impressively, matching the results typically achieved by larger models. While SUT slightly underperformed UT in terms of translation quality (as measured by BLEU score), it significantly outperformed in terms of computational efficiency.
Ablation studies indicated that on this task, MIM loss and MoMHA notably enhanced performance, while ACT loss and halting weren’t as effective.
Compositional Freebase Questions (CFQ): This task involves translating natural language into SPARQL queries, testing compositional generalization. Here, UT performed better than the baselines, especially in computational efficiency, with the best hyperparameters being E=1 and k=1, corresponding to a standard UT rather than SUT.
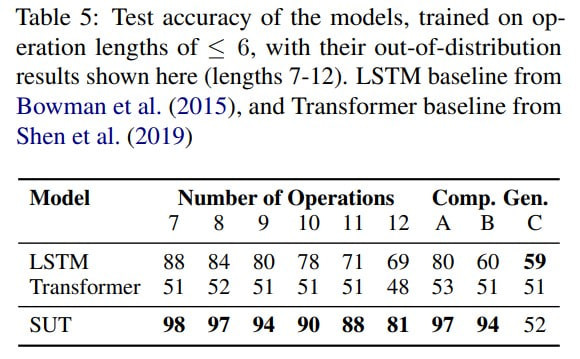
Logical Inference Task: The model was tested with a sequence of logical operators (0-6 in training, 7-12 in testing). Given two logical expressions, the goal
is to predict if the statements are equivalent, contradictory, disjoint, or entail in either direction. This requires the model to learn the hierarchical structure of the problem, which was approached by converting it into a seq2seq translation task. Standard transformers didn’t perform well here; LSTM was a strong baseline, but SUT outperformed it.
Particularly in datasets split for compositional generalization, SUT was the best in two out of three.
As the number of operators increased, the average halting depth grew logically, indicating the model needed "more thinking time".
From additional experiments on the Long Range Arena Listops, SUT outperformed competing transformers.
Post-training Adaptations and Expert Specialization
After training, it's possible to reduce the threshold for the sum of halting probabilities (from the basic 0.999), thus cutting down the volume of computations—a potentially valuable trait for production deployment. This is an impressive feature of ACT in general.
In the Logical Inference task, this adjustment didn't make much difference, as the sum quickly saturates, resulting in approximately a 50% reduction in computations compared to executing all SUT layers. The CFQ task was more intriguing, allowing for a search for some trade-off. Without losing final quality, roughly 20% of computations could be eliminated. In translation tasks, around 9% of computations could be cut.
Analyzing the frequencies with which various experts are chosen for data processing reveals a certain level of expert specialization.
Concluding Thoughts
This is a fascinating direction. While it doesn't yet appear to be a game-changer, the architecture is certainly appealing. Likely, it introduces a more suitable inductive bias for certain tasks.