[S4] Efficiently Modeling Long Sequences with Structured State Spaces
A viable transformer alternative
Authors: Albert Gu, Karan Goel, Christopher Ré
Paper: https://arxiv.org/abs/2111.00396
Code: https://github.com/state-spaces/s4
In the world beyond transformers, there's a lot happening, and the good old RNNs are actively evolving. I've been wanting to write about State Space Models (SSM) and their notable representatives, HiPPO and S4.
The work on S4 was accepted at my favorite conference, ICLR, in 2022, and it received Outstanding Paper Honorable Mentions.
State Space Models (SSM) and HiPPO
A major challenge in the field is modeling long sequences, like those with 10,000 elements or more. Current dominant transformers still struggle with this, primarily due to the quadratic complexity of the attention mechanism (although there are many non-quadratic mechanisms, many of which we've written about).
On this topic, there's the Long Range Arena (LRA) benchmark, where transformers aren't the overall leaders (although the fresh, quasi-transformer, single-headed Mega now leads there, https://arxiv.org/abs/2209.10655).
There have been many approaches to solving the problem of modeling really long sequences, and one of the latest is the state space model (SSM).
SSMs are described by the equations:
x′(t)=Ax(t)+Bu(t)
y(t)=Cx(t)+Du(t)
where u(t) is the input signal, x(t) is the n-dimensional latent representation, y(t) is the output signal, and A, B, C, and D are trainable matrices. It is a bit confusing notation as usually input signal is x(t), and the hidden state (or latent representation) is h(t). This will be fixed in the recent state-of-the-art SSM called Mamba (post coming soon).
In the work on SSMs, D is considered zero, as it's analogous to a skip-connection and easy to compute.
In practice, such a model performs poorly because solving this ODE leads to an exponential function, with all the familiar RNN issues like vanishing/exploding gradients.
The HiPPO framework from NeurIPS 2020 (https://arxiv.org/abs/2008.07669) proposes a special class of matrices A, which allows for better memory of input history. The most important matrix in this class, called the HiPPO Matrix, is:
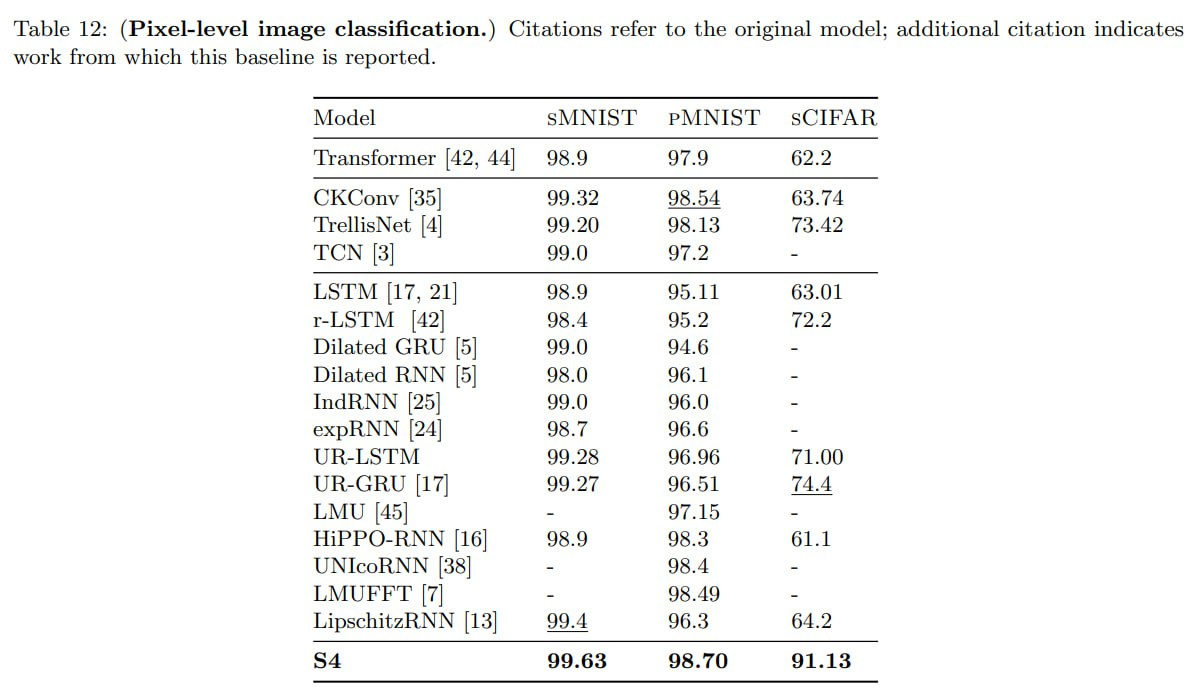
Replacing the random matrix A in SSM with this improves results on sequential MNIST from 60% to 98%.
This is a continuous description, and to apply it to discrete inputs, the SSM needs to be discretized with a step Δ, and the input signal will be sampled with this step. This is done using a bilinear method, replacing the matrix A with its approximation
The state equations now become a recurrent formula with x_k, similar to RNNs, and x_k itself can be seen as a hidden state with the transition matrix A.
There's also a separate hack that this recurrent formula can be unfolded and replaced with a convolution (with a kernel K) the length of the sequence, but I won't bring that formula here as it doesn't look great in text. Such computations can be done quickly on modern hardware.
The bottleneck of discrete-time SSMs is the need to multiply repeatedly by the matrix A.
Structured State Spaces (S4)
The current work proposes an extension and improvement of SSM named Structured State Spaces (S4). A new parameterization is suggested, where the matrix A (the HiPPO matrix) is decomposed into the sum of a low-rank and a normal term, Normal Plus Low-Rank (NPLR).
In addition, several other techniques are applied: truncated SSM generating function + Cauchy kernel + application of the Woodbury identity + calculation of the convolution kernel's spectrum through the truncated generating function + inverse FFT. For details and proofs, welcome to the article.
It's proven that all HiPPO matrices have an NPLR representation, and that the SSM convolutional filter can be computed in O(N + L) operations and memory (and this is the main technical contribution of the paper).
The default S4 works with one input and output number, but in reality, DNNs usually need multidimensional vectors. To support not just one feature but many (H pieces), H independent copies of S4 are made, and the H features are mixed through a position-wise linear layer (i.e., I understand, for each feature, there's such a layer looking at all the other features). This is also similar to depthwise-separable convolutions, and the entire deep (multilayer) S4 is close to a depthwise-separable CNN with a global convolution kernel.
By default, the transformation is linear, but adding nonlinear transformations between layers makes the entire deep SSM nonlinear.
The resulting S4 is compared with LSSL (Linear State-Space Layer, the same authors, https://arxiv.org/abs/2110.13985) and S4 is significantly better, and with efficient transformers (comparable to Performer or Linear Transformer).
At the time of publication, S4 beat a dozen different efficient transformers on LRA. The standard inefficient one as well (although it's good in quality, it's terrible in speed and memory). Since the first publication of the article, it has been updated and the results of S4 have been further improved.
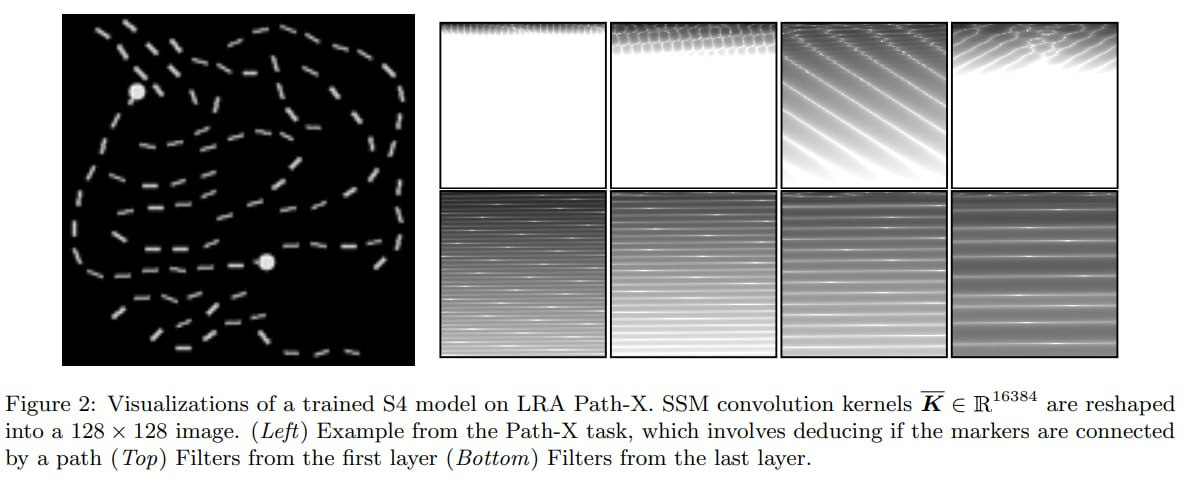
Among other things, S4 solved the Path-X challenge, which hadn't been solved before. In this task, one must determine whether two points are connected by a path in a 128x128 image, which after unfolding the image leads to a sequence length of 16,384. In convolutions, interesting patterns are learned with an "understanding" of two-dimensional data.
It was also tested on a subset of the SC10 tasks from the Speech Commands dataset. No tricky features were used, working with raw speech of 16k length, and it achieved 98.3% accuracy, beating methods using MFCC features.
Among other tasks was the WikiText-103 benchmark, where transformers ruled, and S4 didn't overtake them, but replacing self-attention with S4 only resulted in a difference in perplexity of 0.8, and the inference speed was 60 times higher.
By the way, the current 2nd place on this benchmark (after retrieval augmented RETRO on the 1st place) is H3 or “Hungry Hungry Hippos: Towards Language Modeling with State Space Models” (https://arxiv.org/abs/2212.14052) by the same authors, accepted at ICLR 2023.
In time series prediction tasks, S4 was compared with Informer (a special transformer for time-series) and other baselines. S4 rules in general.
Interesting ablations were conducted, showing that HiPPO initialization is very important, significantly beating Gaussian in both training speed and final quality.
In general, among SSMs there are now many strong representatives, and the topic deserves wide attention.
Some more relevant links on the topic:
“The Annotated S4” with JAX code
Talk by one of the paper authors
Another fresh talk by Albert Gu
A deep-dive talk focused on JAX