Pay Attention to Small Weights

Authors: Chao Zhou, Tom Jacobs, Advait Gadhikar, Rebekka Burkholz
Paper: https://arxiv.org/abs/2506.21374

An interesting topic about the nature of things.

Memory has long been one of the biggest bottlenecks when working with large models. Even if you've downloaded a model with billions of parameters and it fits into your accelerator's memory, that's still not enough. During inference, you need to store activations, and during training and fine-tuning, you also need gradients and optimizer states. When using Adam, for example, you need 3N memory cells for N trainable parameters (storing first and second moments).

There are various approaches to memory optimization, such as checkpointing, quantization, and offloading. Among newer approaches are low-dimensional gradient projections (via SVD), applying Adam in these new spaces, and projecting back to the original space—this is how GaLore works (https://arxiv.org/abs/2403.03507). MicroAdam (https://arxiv.org/abs/2405.15593) keeps top-k gradients and uses error feedback to restore performance. But all of this still requires quite a lot of memory. The proposed new method is also based on the idea of selecting a small subset of parameters for updating, but it doesn't require gradients for parameter selection and doesn't need error feedback.

On small weights

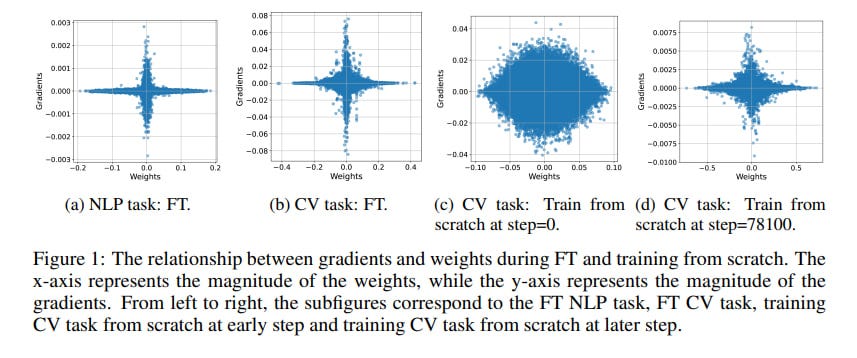
The work is based on an interesting observation—large gradients are usually associated with weights of small magnitude, which is especially pronounced during fine-tuning.

For experiments, they took a BERT-type model and the CoLA dataset from GLUE, as well as a pre-trained ImageNet ViT-Large with fine-tuning on CIFAR-10.

The plots showing weight and gradient distributions during fine-tuning have a star shape, with large spikes in gradient magnitude around near-zero weights. This is visible in both CV and NLP tasks. During training from scratch, this is much less pronounced, but still somewhat noticeable (see Fig. 1). The effect is only unnoticeable in the final classification layer, but this may have explanations (during fine-tuning, the classification head is usually randomly initialized and trained from scratch, and it must adapt to a specific non-universal task).

The authors propose two explanations for such phenomena.

First, after pre-training, large weights likely correspond to some important features that are less subject to change during fine-tuning. Small weights change more for task-oriented features. With randomly initialized weights (when training a network from scratch), this wouldn't be the case. This seems logical.

Second, overparameterization. Perhaps there are already excess weights in the model, so pre-trained large weights don't need to be changed. To investigate this question, they introduced a metric r in the gradient-weight space.

For this metric, the top-k largest gradients by magnitude (g) are determined, and the median of their corresponding weights (w, which are trainable parameters, not their gradients) is calculated. Then it's divided by the maximum absolute weight among the bottom-k parameters by gradient magnitude. This characterizes the hyperbolic trend—if the r value is low, then high gradients correspond to weights with small magnitude. On ViT-Tiny and ViT-Large for the top 0.01% and bottom 80% of weights, the r value is consistently low.

Based on the results, the authors propose an idea—perhaps the magnitude of the parameter, rather than the gradient, is a more effective criterion for selecting a subset of weights for updating during fine-tuning?

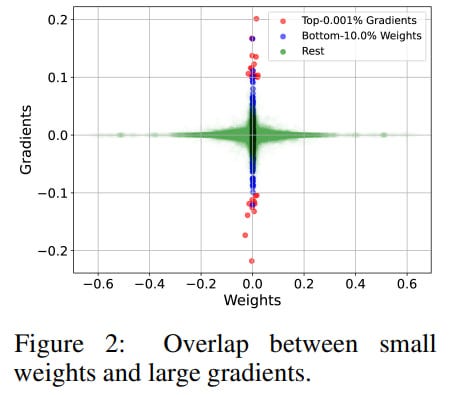
Next, they looked at two subsets: top 0.001% with maximum gradient magnitude and bottom 10% by weight magnitude.

The intersection is quite large but incomplete, so these aren't two sides of the same coin—the difference in quantity between 0.001% and 10% is huge, and something important requiring large gradients remains. But judging by the visualization, they're still not that far from the center of the plot at zero.

The final idea is to focus on updating weights with small magnitude. First, due to overparameterization, this may be sufficient. Second, although the intersection isn't ideal, small weights still provide a good chance of intersecting with large gradients. Finally, large weights likely contain something important from pre-training, so touching them is risky. The authors call this approach to weight updating nano gradient descent.

Here comes nano-optimization

Accordingly, the optimizer based on this idea is called NanoAdam.

In brief, the idea is that we select a subset of parameters that we will train. They are defined by a mask (here, I) that selects from all parameters, and standard Adam updates are performed for them. In addition to the mask, there's a so-called density scheduler that dynamically adjusts the proportion of parameters participating in training (linear decay by default). As a result, the proportion of parameters (k pieces) is updated according to some schedule and a mask is generated (bottom k by weight magnitude), this happens every d and m iterations respectively. It doesn't make sense to update the mask every time—parameters with small magnitude tend to remain so throughout the entire optimization. Moreover, thanks to this, you can preserve the training dynamics with momentum.

Ablations show that the proposed procedure makes sense. If instead of small weights you choose large or random ones, the results are consistently worse. Everything is especially bad with large weights. If you choose weights with large gradients, it also works worse.

They conducted many fine-tuning experiments on NLP tasks with BERT-Base/Large and OPT-1.3B. On average, NanoAdam outperforms alternatives like MicroAdam, Galore, and regular/8bit AdamW. However, confidence intervals are unclear.

Most importantly, it requires less memory. On OPT-1.3B it's 11.6G versus 13G for MicroAdam/Adam-8b, 14G for GaLore, and 18G for AdamW. That's reasonable savings.

They separately tested catastrophic forgetting on CV tasks with ViT and ResNet during continual learning, when they first fine-tuned on CIFAR-10 (Task 1), then on Flowers102 (Task 2). NanoAdam is the champion. I just didn't catch why ResNets have such a large drop on Flowers102.

NanoAdam also led to the smallest parameter change (except for classification heads) by L2 metric (and despite a higher learning rate).

It looks interesting. And I like the from-first-principles approach.