Make softmax great again

softmax is not enough (for sharp out-of-distribution)
Authors: Petar Veličković, Christos Perivolaropoulos, Federico Barbero, Razvan Pascanu
Paper: https://arxiv.org/abs/2410.01104

Let’s go back to warm, insightful reviews that NotebookLM can't yet match. Today, we have an intriguing study that delves (a sign of GPT, yes?) deep into the inner workings of neural networks.

As is known, the default attention mechanism within transformers uses softmax to calculate final attention weights. Softmax converts a vector of logits with arbitrary values into a probability distribution, where everything sums to one. It can also include temperature to modify this distribution (a good visualization of temperature is available here).

The best way to understand transformer

Softmax is often used in classifiers' outputs and frequently within transformers. Some research attributes its success to its ability to model circuits (see Distill), which is beneficial for interpretability within transformers.

In this paper, the authors focus on the out-of-distribution scenario, where a trained model has to work with data distributions that differ from those it was trained on, which is particularly important for reasoning engines. And here lies the issue with softmax.

Consider a model case—a simple architecture with a single attention head. The task: predicting the element with the highest value in a set (max retrieval task). The element’s features are processed by an MLP before entering the attention block and then proceed to an output MLP for final prediction. Training is performed on sets of up to 16 elements. During inference, the model is tested on significantly larger sets, up to 2¹¹ elements.

Visualization of attention weights shows good performance on sizes comparable to training, but beyond that, the distribution quickly blurs into uniformity.

An experiment on a trained Gemma 2B model replicates this: as the input size grows, so does the entropy (used as a proxy for sharpness) of the heads. A lemma and theorem are proven, confirming that as the number of input elements increases with a fixed input vocabulary size, softmax indeed blurs.

To “make softmax great again,” the authors propose using adaptive temperature to resolve this and make softmax sharper. Recall, the lower the temperature, the closer softmax approaches hard attention—a maximally sharp distribution. However, transformers don’t perform well with zero temperature. Applying zero temperature to an already trained transformer is also ineffective. An attention head that has learned to produce a sharp distribution does so by increasing the magnitude of weights, which leads to overfitting and a higher probability of selecting the wrong token. Setting the temperature to zero would reduce accuracy in this scenario.

Instead, we might want to make the input coefficients sharper, and here, the authors suggest adaptive temperature based on the entropy of the input coefficients. Lowering the temperature monotonically decreases entropy.

To construct the adaptive temperature function, the authors first generated a dataset of inputs where the maximum element does not receive the highest probability. They identified the temperature value that maximized this probability and fitted a fourth-degree polynomial to determine temperature based on entropy.

This temperature function is used during inference as a drop-in replacement for the standard jax.nn.softmax().

I’m not entirely sure why a trainable temperature wouldn’t work here. It seems it would add only a minor number of parameters—just one scalar per softmax. If examining the input distribution is necessary, one could use an MLP, which would add more parameters but could be shared across all softmax operations. It doesn’t seem like a big deal. Years ago, I thought about trying something like this, and I’m sure it has been attempted many times—here’s a relevant paper I found quickly: arXiv:2302.06130. This approach also seems logical, as a similar case was discussed some time ago here. It’s unclear why they took a more complicated route with fourth-degree polynomials…

Anyway, they tested it on the same max retrieval task. With adaptive temperature (modified only during inference), performance improved slightly and statistically significantly. Visualizations of attention also became a bit sharper for longer inputs, though not drastically so.

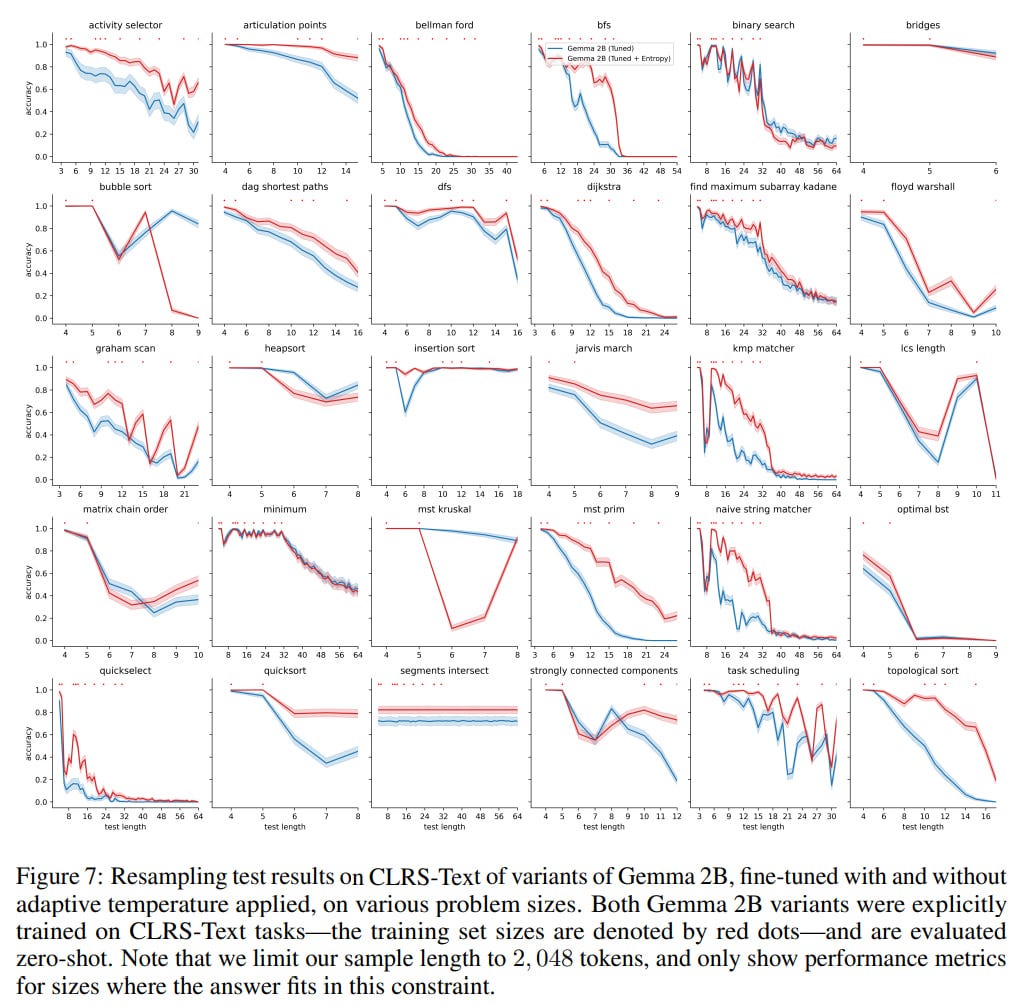
They also tested on the Gemma 2B model and the CLRS-Text benchmark for algorithmic reasoning (arXiv:2406.04229). This dataset is more complex, containing many floating-point numbers split into multiple tokens, where focusing on a single correct token isn’t very effective. They could have fitted a polynomial again following the same procedure, but for the multi-headed Gemma, this is more complicated—understanding what the heads do is already challenging. So here, they opted to learn the temperature. Voilà. This part of the work is poorly described; it’s unclear what exactly was implemented—whether it was a learnable temperature, the same fixed polynomial but with learned coefficients, the fixed polynomial coefficients with the network learned to work with it, or another approach. Regardless, performance improved on most tasks.

Overall, I feel that we are close to this kind of work being created by a system like o1 (or maybe its next version, say, o2) or a smart new Claude 3.5 (or the future 4.0), possibly within a multi-agent architecture. I have to look deeper into what AI Scientist (arXiv:2408.06292) has generated to see if it was comparable or not.

In general, the authors believe their main contribution is not just adaptive temperature but highlighting the need to consider alternatives to softmax in light of their proposed theory. Non-normalized attention variants (including linear) face challenges in ranking elements. Hard or local attentions lie outside this theory’s scope. While these approaches haven’t yielded remarkable results in typical transformers yet, perhaps we simply haven’t learned to use them effectively. Interesting hybrids may emerge. The authors especially hope for improvements in reasoning.